
【题目】如图,菱形ABCD的对角线AC与BD交于点O,AB=5,AC=6,点E,F分别在AD,CD上,AE=CF= ![]() ,EF交BD于点H.将△DEF沿EF折到△
,EF交BD于点H.将△DEF沿EF折到△ ![]() 的位置,
的位置, ![]() .
.
(1)证明: ![]() 平面ABCD;
平面ABCD;
(2)求二面角 ![]() 的正弦值.
的正弦值.
【答案】
(1)
证明:∵ ![]() ,
,
∴ ![]() ,
,
∴ ![]() .
.
∵四边形 ![]() 为菱形,
为菱形,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() .
.
∵ ![]() ,
,
∴ ![]() ;
;
又 ![]() ,
, ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() .
.
又∵ ![]() ,
,
∴ ![]() 面
面 ![]()
(2)
解:建立如图坐标系 ![]() .
.

![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
设面 ![]() 法向量
法向量 ![]() ,
,
由  得
得 ![]() ,取
,取  ,
,
∴ ![]() .
.
同理可得面 ![]() 的法向量
的法向量 ![]() ,
,
∴  ,
,
∴ ![]()
【解析】(1)由底面ABCD为菱形,可得AD=CD,结合AE=CF可得EF∥AC,再由ABCD是菱形,得AC⊥BD,进一步得到EF⊥BD,由EF⊥DH,可得EF⊥D′H,然后求解直角三角形得D′H⊥OH,再由线面垂直的判定得D′H⊥平面ABCD;(2)以H为坐标原点,建立如图所示空间直角坐标系,由已知求得所用点的坐标,得到 ![]() 的坐标,分别求出平面ABD′与平面AD′C的一个法向量
的坐标,分别求出平面ABD′与平面AD′C的一个法向量 ![]() ,设二面角二面角B﹣D′A﹣C的平面角为θ,求出|cosθ|.则二面角B﹣D′A﹣C的正弦值可求
,设二面角二面角B﹣D′A﹣C的平面角为θ,求出|cosθ|.则二面角B﹣D′A﹣C的正弦值可求


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分13分)在四棱锥![]() 中,
中, ![]() ,
, ![]()
![]() ,
, ![]() 平面
平面![]() ,直线PC与平面ABCD所成角为
,直线PC与平面ABCD所成角为![]() ,
, ![]() .
.

(Ⅰ)求四棱锥![]() 的体积
的体积![]() ;
;
(Ⅱ)若![]() 为
为![]() 的中点,求证:平面
的中点,求证:平面![]()
![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,按其数学成绩(均为整数)分成六组![]() ,
, ![]() ,…,
,…, ![]() 后得到如下部分频率分布直方图,观察图中的信息,回答下列问题:
后得到如下部分频率分布直方图,观察图中的信息,回答下列问题:
(1)补全频率分布直方图;
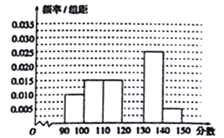
(2)估计本次考试的数学平均成绩(同一组中的数据用该组区间的中点值作代表);
(3)用分层抽样的方法在分数段为![]() 的学生成绩中抽取一个容量为6的样本,再从这6个样本中任取2人成绩,求至多有1人成绩在分数段
的学生成绩中抽取一个容量为6的样本,再从这6个样本中任取2人成绩,求至多有1人成绩在分数段![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若将函数y=2sin 2x的图像向左平移 ![]() 个单位长度,则评议后图象的对称轴为( )
个单位长度,则评议后图象的对称轴为( )
A.x= ![]() –
– ![]() (k∈Z)
(k∈Z)
B.x= ![]() +
+ ![]() (k∈Z)
(k∈Z)
C.x= ![]() –
– ![]() (k∈Z)
(k∈Z)
D.x= ![]() +
+ ![]() (k∈Z)
(k∈Z)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】α、β是两个平面,m、n是两条直线,有下列四个命题:
①如果m⊥n , m⊥α , n∥β , 那么α⊥β.
②如果m⊥α , n∥α , 那么m⊥n.
③如果α∥β , m ![]() α , 那么m∥β.
α , 那么m∥β.
④如果m∥n , α∥β , 那么m与α所成的角和n与β所成的角相等.
其中正确的命题有.(填写所有正确命题的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() 的焦点在
的焦点在 ![]() 轴上,A是E的左顶点,斜率为k(k>0)的直线交E于A,M两点,点N在E上,MA⊥NA.
轴上,A是E的左顶点,斜率为k(k>0)的直线交E于A,M两点,点N在E上,MA⊥NA.
(1)当t=4, ![]() 时,求△AMN的面积;
时,求△AMN的面积;
(2)当 ![]() 时,求k的取值范围.
时,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在长方形![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 为线段
为线段![]() 上一动点.现将
上一动点.现将![]() 沿
沿![]() 折起,形成四棱锥
折起,形成四棱锥![]() .
.



图1 图2 图3
(Ⅰ)若![]() 与
与![]() 重合,且
重合,且![]() (如图2).
(如图2).
(ⅰ)证明:![]() 平面
平面![]() ;
;
(ⅱ)求二面角![]() 的余弦值.
的余弦值.
(Ⅱ)若![]() 不与
不与![]() 重合,且平面
重合,且平面![]() 平面
平面![]() (如图3),设
(如图3),设![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从含有两件正品a,b和一件次品c的3件产品中每次任取一件,连续取两次,求取出的两件产品中,恰有一件是次品的概率。
(1)每次取出不放回;(2)每次取出放回;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com