
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据平面向量的基本概念,对选项中的命题进行分析、判断即可.
解答 解:对于①,当$\overrightarrow{a}$•$\overrightarrow{b}$=0时,$\overrightarrow{a}$=$\overrightarrow{0}$或$\overrightarrow{b}$=$\overrightarrow{0}$或$\overrightarrow{a}$⊥$\overrightarrow{b}$,∴①错误;
对于②,当|$\overrightarrow{a}$|=|$\overrightarrow{b}$|时,($\overrightarrow{a}$+$\overrightarrow{b}$)•($\overrightarrow{a}$-$\overrightarrow{b}$)=${\overrightarrow{a}}^{2}$-${\overrightarrow{b}}^{2}$=|${\overrightarrow{a}}^{2}$|-|${\overrightarrow{b}}^{2}$|=0,∴②正确;
对于③,当$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$时,$\overrightarrow{a}$•$\overrightarrow{b}$-$\overrightarrow{a}$•$\overrightarrow{c}$=$\overrightarrow{a}$•($\overrightarrow{b}$-$\overrightarrow{c}$)=0,∴$\overrightarrow{a}$=$\overrightarrow{0}$或$\overrightarrow{b}$-$\overrightarrow{c}$=$\overrightarrow{0}$或$\overrightarrow{a}$⊥($\overrightarrow{b}$-$\overrightarrow{c}$),∴③错误;
对于④,当$\overrightarrow{b}$=$\overrightarrow{0}$时,有$\overrightarrow{a}$∥$\overrightarrow{b}$,$\overrightarrow{b}$∥$\overrightarrow{c}$,但$\overrightarrow{a}$∥$\overrightarrow{c}$不一定成立,∴④错误;
综上,正确的命题个数为1.
故选:A.
点评 本题考查了平面向量的基本概念与应用问题,是基础题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
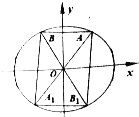 已知离心率为$\frac{1}{2}$的椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),右焦点到椭圆上的点的距离的最大值为3.
已知离心率为$\frac{1}{2}$的椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),右焦点到椭圆上的点的距离的最大值为3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sinx | B. | y=-|x+1| | C. | y=ln$\frac{1-x}{1+x}$ | D. | y=$\frac{1}{2}$(ex+e-x) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{{e}^{2}+1}{e}$) | B. | ($\frac{{e}^{2}+1}{e}$,+∞) | C. | (-$\frac{{e}^{2}+1}{e}$,-2) | D. | (2,$\frac{{e}^{2}+1}{e}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 某电子商务公司对1000名网络购物者2015年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.在这些购物者中,消费金额在区间[0.5,0.9]内的购物者的人数为600.
某电子商务公司对1000名网络购物者2015年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.在这些购物者中,消费金额在区间[0.5,0.9]内的购物者的人数为600.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com