[题目]如图所示.图①是棱长为1的小正方体.图②.③是由这样的小正方体摆放而成．按照这样的方法继续摆放.由上而下分别将第1层.第2层.-.第层的小正方体的个数记为.解答下列问题:(1)按照要求填表:1234-136 -(2) ．题目和参考答案——青夏教育精英家教网—

【题目】如图所示，图①是棱长为1的小正方体，图②，③是由这样的小正方体摆放而成．按照这样的方法继续摆放，由上而下分别将第1层，第2层，…，第层的小正方体的个数记为，解答下列问题：

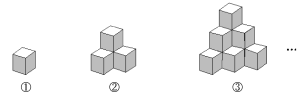
（1）按照要求填表：

	1	2	3	4	…
	1	3	6	_	…

（2）__________．

【答案】10

【解析】

（1）图①有1层，共1个正方体，图②有2层，共个正方体，图③有3层，共+3个正方体，依次类推，第4个图有4层，共个正方体.

（2）由（1）猜想：第个图有层，共个正方体.

（1）图①有1层，第1层正方体的个数为；

图②有2层，第2层正方体的个数为；

图③有3层，第3层正方体的个数为；

依次类推，第4个图有4层，第4层正方体的个数为.

（2）由（1）猜想：第个图有层，第层正方体的个数为.

练习册系列答案

中考导学案系列答案

中考大提速系列答案

中考专题通系列答案

中考第三轮复习冲刺专用模拟试卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】下列随机事件：

①某射手射击一次，可能命中环，环，环，，环；

②一个小组有男生人，女生人，从中任选人进行活动汇报；

③一只使用中的灯泡寿命长短；

④抛出一枚质地均匀的硬币，观察其出现正面或反面的情况；

⑤中秋节前夕，某市有关部门调查辖区内某品牌的月饼质量，给该品牌月饼评“优”或“差”.

这些事件中，属于古典概型的是________.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某公司有员工1000名，平均每人每年创造利润10万元．为了增加企业竞争力，决定优化产业结构，调整出名员工从事第三产业，调整后他们平均每人每年创造利润为万元（），剩下的员工平均每人每年创造的利润可以提高．

（1）若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润，则调整员工从事第三产业的人数应在什么范围？

（2）在（1）的条件下，若调整出的员工创造的年总利润始终不高于剩余员工创造的年总利润，求的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，三棱柱的各棱长均为2，面，E，F分别为棱的中点．

（1）求证：直线BE∥平面；

（2）平面与直线AB交于点M，指出点M的位置，说明理由，并求三棱锥的体积．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数（其中）．

（1）当时，判断零点的个数k；

（2）在（1）的条件下，记这些零点分别为，求证：．

查看答案和解析>>

科目：高中数学 来源： 题型：

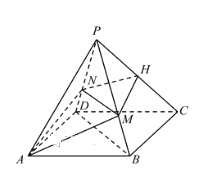
【题目】已知四棱锥，底面为菱形，为上的点，过的平面分别交于点，且平面．

（1）证明：；

（2）当为的中点，，与平面所成的角为，求平面AMHN与平面ABCD所成锐二面角的余弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】计划在某水库建一座至多安装3台发电机的水电站，过去50年的水文资料显示，水库年入流量(年入流量：一年内上游来水与库区降水之和.单位：亿立方米）都在40以上.其中，不足80的年份有10年，不低于80且不超过120的年份有35年，超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率，并假设各年的年入流量相互独立.