
分析 (1)由题意可得,只需证(a+b+c)2≥3,只需证a2+b2+c2≥1,只需证a2+b2+c2-(ab+bc+ca)≥0,只需证(a-b)2+(b-c)2+(c-a)2≥0.
(2)由题意得 ${(m+|{x-1}|+|{x+1}|)_{min}}≤{(a+b+c)^2}_{min}$,即可求m的取值范围.
解答 (1)证明:要证原不等式成立,只需证(a+b+c)2≥3,即证a2+b2+c2+2(ab+bc+ca)≥3,
又ab+bc+ca=1.所以,只需证:a2+b2+c2≥1,即a2+b2+c2-1≥0,
因为ab+bc+ca=1.所以,只需证:a2+b2+c2-(ab+bc+ca)≥0,
只需证:2a2+2b2+2c2-2(ab+bc+ca)≥0,
即(a-b)2+(b-c)2+(c-a)2≥0,而(a-b)2+(b-c)2+(c-a)2≥0显然成立,
故原不等式成立;
(2)解:由题意得 ${(m+|{x-1}|+|{x+1}|)_{min}}≤{(a+b+c)^2}_{min}$
由(1)知(a+b+c)2min=3,
又|x-1|+|x+1|≥|(x-1)-(x+1)|=2,∴m+2≤3,m的取值范围为:m≤1.
点评 本题考查基本不等式,绝对值不等式的性质,恒成立,能成立综合问题,用分析法证明不等式,寻找使不等式成立的充分条件,是解题的关键.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$ | B. | $\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}•\overrightarrow{n}|}$ | C. | -$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}||\overrightarrow{n}|}$ | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
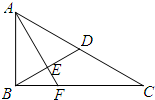 如图,△ABC中,∠ABC=90°,∠C=30°,AB=1,D为AC中点,AE⊥BD于点E,延长AE交BC于点F,沿BD将△ABC折成四面体A-BCD.
如图,△ABC中,∠ABC=90°,∠C=30°,AB=1,D为AC中点,AE⊥BD于点E,延长AE交BC于点F,沿BD将△ABC折成四面体A-BCD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 等腰三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{3}$ | B. | $2\sqrt{2}$ | C. | $2\sqrt{5}$ | D. | $2\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com