
分析 (Ⅰ)由数列的递推式:当n=1时,a1=S1;当n≥2时,an=Sn-Sn-1,计算即可得到所求通项;
(Ⅱ)由(Ⅰ)得${b_n}={2^{2n-5}}+1$.运用数列的求和方法:分组求和,结合等比数列的求和公式,计算即可得到所求和;
(Ⅲ)运用数列的求和方法:裂项相消求和,化简整理,判断数列的最值,再由恒成立思想,即可得到所求实数λ的最小值.
解答 解:(Ⅰ)当n=1时,a1=S1=-3;
当n≥2时,an=Sn-Sn-1=n2-4n-(n-1)2+4(n-1)=2n-5,
因为a1=-3符合上式,
所以an=2n-5(n∈N*).
(Ⅱ)由(Ⅰ)得${b_n}={2^{2n-5}}+1$.
所以Tn=b1+b2+…+bn=(2-3+1)+(2-1+1)+…+(22n-5+1)
=(2-3+2-1+…+22n-5)+n
=$\frac{{{2^{-3}}(1-{4^n})}}{1-4}+n$=$\frac{1}{24}({4^n}-1)+n$.
(Ⅲ)$\frac{1}{{{a_1}{a_2}}}+\frac{1}{{{a_2}{a_3}}}+…+\frac{1}{{{a_n}{a_{n+1}}}}=\frac{1}{3}-1+\frac{1}{1×3}+\frac{1}{3×5}+…+\frac{1}{(2n-5)(2n-3)}$
=$-\frac{2}{3}+\frac{1}{2}[(1-\frac{1}{3})+(\frac{1}{3}-\frac{1}{5})+…+(\frac{1}{2n-5}-\frac{1}{2n-3})]$=$-\frac{1}{6}-\frac{1}{4n-6}$,
当n=1时,$\frac{1}{{{a_1}{a_2}}}=\frac{1}{3}$,(注:此时$\frac{1}{4n-6}<0$),
当n≥2时,因为$\frac{1}{4n-6}>0$,
所以$\frac{1}{{{a_1}{a_2}}}+\frac{1}{{{a_2}{a_3}}}+…+\frac{1}{{{a_n}{a_{n+1}}}}<-\frac{1}{6}$.
则n=1时,取得最大值.
因为对于任意正整数n,都有$\frac{1}{{{a_1}{a_2}}}+\frac{1}{{{a_2}{a_3}}}+…+\frac{1}{{{a_n}{a_{n+1}}}}≤λ$,
由题意,得$λ≥\frac{1}{3}$;
所以λ的最小值为$\frac{1}{3}$.
点评 本题考查数列的通项公式的求法,注意运用数列的递推式,考查数列的求和方法:分组求和和裂项相消求和,以及数列的最值,考查运算能力,属于中档题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥P-ABCD中,已知DC∥AB,DC=2AB,E为棱PD的中点.
在四棱锥P-ABCD中,已知DC∥AB,DC=2AB,E为棱PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1<k<1 | B. | 1<k<$\sqrt{2}$ | C. | 1<k<2 | D. | $\sqrt{2}$<k<2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
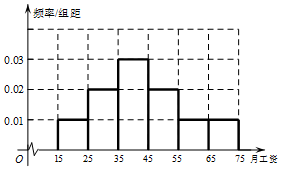 为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表和频率分布直方图:
为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表和频率分布直方图:| 月工资 (单位:百元) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 男员工数 | 1 | 8 | 10 | 6 | 4 | 4 |
| 女员工数 | 4 | 2 | 5 | 4 | 1 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${a_5}^2={a_3}•{a_7}$ | B. | ${a_5}^2={a_1}•{a_9}$ | ||
| C. | ${a_n}^2={a_{n-1}}•{a_{n+1}}({n∈{N^*}})$ | D. | ${a_n}^2={a_{n-k}}•{a_{n+k}}({k∈{N^*},n>k>0})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com