
| y1-y2 |
| x1-x2 |


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:
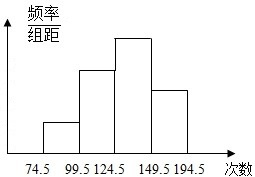 为了解学生的体能情况,抽取了一个学校的部分学生进行一分钟跳绳次数测试,将所得数据整理成统计图如图,已知图中从左到右各个小组的高度之比分别为1:3:4:2,最左边一组的频数为5,请根据以上信息和图形解决以下问题:
为了解学生的体能情况,抽取了一个学校的部分学生进行一分钟跳绳次数测试,将所得数据整理成统计图如图,已知图中从左到右各个小组的高度之比分别为1:3:4:2,最左边一组的频数为5,请根据以上信息和图形解决以下问题:查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 6 |
| 5π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 2 |
| 1 |
| a |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 3 |
| 4 |
| 7 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 2 |
| k |
| x+2 |
| k |
| x+2 |
| k |
| x+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M、N均在直线x=6上,圆弧C1的圆心是坐标原点O,半径为10,圆弧C2过点A(38,0).
如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M、N均在直线x=6上,圆弧C1的圆心是坐标原点O,半径为10,圆弧C2过点A(38,0).| 39 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某校高三年级有500名同学,将他们的身高(单位:cm)数据绘制成频率分布直方图(如图),现用分层抽样的方法选取x名学生参加某项课外活动,已知从身高在[160,170)的学生中选取9人,则x=
某校高三年级有500名同学,将他们的身高(单位:cm)数据绘制成频率分布直方图(如图),现用分层抽样的方法选取x名学生参加某项课外活动,已知从身高在[160,170)的学生中选取9人,则x=查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com