
(本小题满分14分)
设函数
(I)当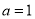 时,求函数
时,求函数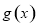 的单调区间;
的单调区间;
(II)若对任意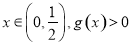 恒成立,求实数
恒成立,求实数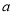 的最小值;
的最小值;
(III)设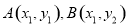 是函数
是函数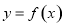 图象上任意不同两点,线段AB中点为C
图象上任意不同两点,线段AB中点为C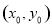 ,直线AB的斜率为k.证明:
,直线AB的斜率为k.证明: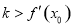 .
.
(Ⅰ) 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为 ; (Ⅱ)
; (Ⅱ) ;(Ⅲ)详见解析
;(Ⅲ)详见解析
【解析】
试题分析:(I)将 代入函数解析式,可得
代入函数解析式,可得 根据导数在函数单调性中的应用,即可求出
根据导数在函数单调性中的应用,即可求出 的单调递增,递减区间. (Ⅱ)由题意知:
的单调递增,递减区间. (Ⅱ)由题意知: ,在
,在 时恒成立,即
时恒成立,即 在区间
在区间 上恒成立,又
上恒成立,又 ,利用分离参数法,可得
,利用分离参数法,可得 在区间
在区间 上恒成立.构造辅助函数,再利用函数的单调性,即可求出结果;(Ⅲ) 由于
上恒成立.构造辅助函数,再利用函数的单调性,即可求出结果;(Ⅲ) 由于 ,又
,又 ,所以
,所以 ,即证
,即证 ,不妨设
,不妨设 ,即证:
,即证: ,即证:
,即证: ,设
,设 ,即证:
,即证: ,构造辅助函数,利用函数的单调性即可证明结果.
,构造辅助函数,利用函数的单调性即可证明结果.
试题解析:(I)当 时,
时,
当 时,
时, 单调递减;
单调递减;
当 时,
时, 单调递增,
单调递增,
综上, 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为 .
.
(Ⅱ)由题意知: ,在
,在 时恒成立,
时恒成立,
即 在区间
在区间 上恒成立,
上恒成立,
又 ,
, 在区间
在区间 上恒成立.
上恒成立.
设 ,
, ,
,
又令 ,则
,则
当 时,
时, 单调递减,
单调递减,
 ,即
,即 在区间
在区间 恒成立,
恒成立,
所以 在区间
在区间 单调递增,
单调递增, ,
,
故 .
.
(Ⅲ)证明: 又
又
所以 ,即证
,即证
不妨设 ,即证:
,即证: ,
,
即证: ,设
,设 ,即证:
,即证: ,
,
也就是要证: ,其中
,其中
事实上:设 ,
,
则
所以 在
在 单调递增,因此
单调递增,因此 ,即结论成立.
,即结论成立.
考点:1.导数在函数单调性中的应用;2. 导数在函数最值的应用;3. 导数证明不等式中的应用.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案科目:高中数学 来源:2014-2015学年吉林省长春市高三质量监测(二)文科数学试卷(解析版) 题型:选择题
复数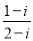 对应的点位于( )
对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省资阳市高三第二次诊断性考理科数学试卷(解析版) 题型:选择题
在不等式组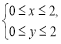 所表示的平面区域内任取一点P,若点P的坐标(x,y)满足
所表示的平面区域内任取一点P,若点P的坐标(x,y)满足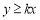 的概率为
的概率为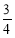 ,则实数k=( )
,则实数k=( )
(A) 4 (B)2
(C)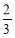 (D)
(D)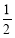
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省潍坊市高三上学期期末考试文科数学试卷B卷(解析版) 题型:解答题
(本小题满分12分)
某中学举行了一次“社会主义核心价值观知识竞赛”活动,为了解本次竞赛中学生成绩情况,从全体学生中随机抽取了部分学生的分数(得分取整数且不低于50分,满分100分),作为样本(样本容量为n)进行统计.按照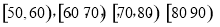
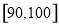 的分组作出频率分布直方图,并作出茎叶图(图中仅列出来
的分组作出频率分布直方图,并作出茎叶图(图中仅列出来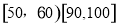 这两组的数据).
这两组的数据).
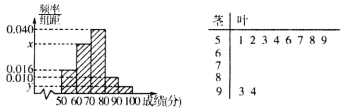
(I)求样本容量n和频率分布直方图中的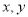 ;
;
(II)在选取的样本中,从样本中竞赛成绩80分以上(含80分)的同学中随机抽取2名同学到市政广场参加社会主义核心价值观知识宣传志愿者活动.求所抽取的2名同学来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省潍坊市高三上学期期末考试文科数学试卷B卷(解析版) 题型:解答题
某公司生产甲、乙两种桶装产品,已知生产甲产品1桶需耗A原料3千克,B原料1千克;生产乙产品1桶需耗A原料1千克,B原料3千克.每生产一桶甲产品的利润400元,每生产一桶乙产品的利润300元.公司在生产这两种产品的计划中,每天消耗A、B原料都不超过12千克,通过合理安排生产计划,公司每天可获得的最大利润是(单位:元)( )
A.1600 B.2100 C.2800 D.4800
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省潍坊市高三上学期期末考试理科数学试卷B卷(解析版) 题型:选择题
向图中边长为2的正方形中,随机撒一粒黄豆,则黄豆落在图中阴影部分的概率为
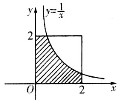
A. 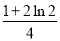 B.
B. 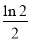
C. 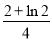 D.
D. 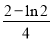
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com