练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆的离心率为，且过点.

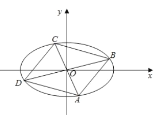
    （1）求椭圆的标准方程；

    （2）四边形的顶点在椭圆上，且对角线、过原点，若，求证；四边形的面积为定值.

    【答案】（1）；（2）

    【解析】

    （1）通过离心率，可得与的关系；再利用点，得到与的关系；通过方程组求得椭圆方程；（2）假设直线方程，与椭圆方程联立，通过根与系数关系可得和的关系；再结合椭圆的对称性，将四边形面积转化为求解的面积。利用弦长公式和点到直线距离公式，将表示出来，整理为定值，从而可证得四边形面积为定值。

    由题意，，又

    解得：，

    椭圆的标准方程为

    （2）①当直线斜率不存在时，设直线方程为

    设，

    又

    ②当直线斜率存在时，设直线的方程为

    设，

    联立，得

    ……①

    ，

    ，即，

    又

    整理可得：

    设原点到直线的距离为，则

    综上所述，四边形面积为定值

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】下列命题是真命题的是(　　)

    A. φ∈R，函数f(x)＝sin(2x＋φ)都不是偶函数

    B. α，β∈R，使cos(α＋β)＝cosα＋cosβ

    C. 向量a＝(2,1)，b＝(－1,0)，则a在b的方向上的投影为2

    D. “|x|≤1”是“x≤1”的既不充分又不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2018年2月22日上午，山东省省委、省政府在济南召开山东省全面展开新旧动能转换重大工程动员大会，会议动员各方力量，迅速全面展开新旧动能转换重大工程.某企业响应号召，对现有设备进行改造，为了分析设备改造前后的效果，现从设备改造前后生产的大量产品中各抽取了200件产品作为样本，检测一项质量指标值，若该项质量指标值落在内的产品视为合格品，否则为不合格品.图3是设备改造前的样本的频率分布直方图，表1是设备改造后的样本的频数分布表.

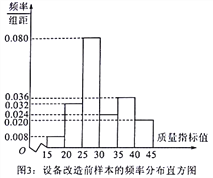
    表1：设备改造后样本的频数分布表

    （1）完成下面的列联表，并判断是否有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关；

    （2）根据图3和表1提供的数据，试从产品合格率的角度对改造前后设备的优劣进行比较；

    （3）企业将不合格品全部销毁后，根据客户需求对合格品进行等级细分，质量指标值落在内的定为一等品，每件售价240元；质量指标值落在或内的定为二等品，每件售价180元；其它的合格品定为三等品，每件售价120元.根据表1的数据，用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品，设其支付的费用为（单位：元），求的分布列和数学期望.

    附：

    0.150

    0.100

    0.050

    0.025

    0.010

    2.072

    2.706

    3.841

    5.024

    6.635

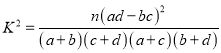
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在△ABC中，AB⊥AC，若AD⊥BC，则AB2＝BD·BC；类似地有命题：在三棱锥A－BCD中，AD⊥平面ABC，若A点在平面BCD内的射影为M，则有S＝S△BCM·S△BCD.上述命题是 (　　)

    A. 真命题

    B. 增加条件“AB⊥AC”才是真命题

    C. 增加条件“M为△BCD的垂心”才是真命题

    D. 增加条件“三棱锥A－BCD是正三棱锥”才是真命题

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝x2－2(a＋2)x＋a2，g(x)＝－x2＋2(a－2)x－a2＋8.设H1(x)＝max，H2(x)＝min (max表示p，q中的较大值，min表示p，q中的较小值)．记H1(x)的最小值为A，H2(x)的最大值为B，则A－B＝(　　)

    A.16B.－16

    C.a2－2a－16D.a2＋2a－16

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知全集为R，设集合A={x|（x+2）（x-5）≤0}，，C={x|a+1≤x≤2a-1}．

    （1）求A∩B，（CRA）∪B；

    （2）若C（A∩B），求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点，圆。

    （1）若点在圆内，求的取值范围；

    （2）若过点的圆的切线只有一条，求切线的方程；

    （3）当时，过点的直线被圆截得的弦长为，求直线的方程。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知分别是双曲线的左、右焦点，过点作垂直与轴的直线交双曲线于，两点，若为锐角三角形，则双曲线的离心率的取值范围是_______．

    【答案】

    【解析】

    根据双曲线的通径求得点的坐标，将三角形为锐角三角形，转化为，即，将表达式转化为含有离心率的不等式，解不等式求得离心率的取值范围.

    根据双曲线的通径可知，由于三角形为锐角三角形，结合双曲线的对称性可知，故，即，即，解得，故离心率的取值范围是.

    【点睛】

    本小题主要考查双曲线的离心率的取值范围的求法，考查双曲线的通径，考查双曲线的对称性，考查化归与转化的数学思想方法，属于中档题.本小题的主要突破口在将三角形为锐角三角形，转化为，利用列不等式，再将不等式转化为只含离心率的表达式，解不等式求得双曲线离心率的取值范围.

    【题型】填空题
    【结束】
    17

    【题目】已知命题：方程有两个不相等的实数根；命题：不等式的解集为.若或为真，为假，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从某市主办的科技知识竞赛的学生成绩中随机选取了40名学生的成绩作为样本，已知这些成绩全部在40分至100分之间，现将成绩按如下方式分成6组：第一组；第二组；；第六组，并据此绘制了如图所示的频率分布直方图．

    求成绩在区间内的学生人数；

    估计这40名学生成绩的众数和中位数．

    查看答案和解析>>

    同步练习册答案