Question

13．设点P在圆x²+（y-6）²=5上，点Q在抛物线x²=4y上，则|PQ|的最小值为$\sqrt{5}$．

Answer 1

分析 设圆心为C，则当|PQ|最小时，P，Q，C三点共线，即|PQ|=|CQ|-|CP|=|CQ|-$\sqrt{5}$，求出|CP|的最小值，即可得出结论

解答 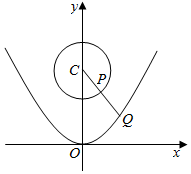解：设点Q（x，y），则x²=4y，
圆x²+（y-6）²=5的圆心C（0，6），半径r=$\sqrt{5}$，
由圆的对称性可得，当|PQ|的最小时，C，P，Q三点共线，即|PQ|=|CQ|-|CP|．
∴|PQ|=$\sqrt{{x}^{2}+（y-6）^{2}}$-$\sqrt{5}$=$\sqrt{{y}^{2}-8y+36}$-$\sqrt{5}$=$\sqrt{（y-4）^{2}+20}$-$\sqrt{5}$≥2$\sqrt{5}$-$\sqrt{5}$=$\sqrt{5}$．
故答案为$\sqrt{5}$．

点评 本题考查抛物线上的动点和圆上的动点间的距离的最小值，解题时要认真审题，注意两点间距离公式和配方法的灵活运用．