
分析 (I)根据焦点坐标求出p,从而得出M点坐标,对直线l有无斜率进行讨论,分两种情况求出l方程;
(II)直线l有无斜率进行讨论,分两种情况得出面积关于l的斜率k的函数,从而得出面积的最小值.
解答 解:(I)∵抛物线C:y2=2px(p>0)的焦点为F(1,0),∴p=2.
∴抛物线E的焦点为M(0,1).
当直线l无斜率时,直线l的方程为x=0,显然直线l与抛物线C只有一个交点(0,0),符合题意.
当直线l有斜率时,设直线l的方程为:y=kx+1,
联立方程组$\left\{\begin{array}{l}{y=kx+1}\\{{y}^{2}=4x}\end{array}\right.$,消元得:k2x2+(2k-4)x+1=0,
∵直线l与抛物线C有且只有一个交点,
∴△=(2k-4)2-4k2=0,解得k=1.
∴直线l的方程为y=x+1.
综上,直线l的方程为x=0或y=x+1.
(II)当直线l无斜率时,直线l的方程为x=1,
联立方程组$\left\{\begin{array}{l}{{y}^{2}=4x}\\{x=1}\end{array}\right.$,解得A(1,-2),B(1,2).
∴S△AOB=$\frac{1}{2}×OF×AB$=2.
当直线l有斜率时,设直线l方程为y=k(x-1).
联立方程组$\left\{\begin{array}{l}{{y}^{2}=4x}\\{y=k(x-1)}\end{array}\right.$,消元得:y2-$\frac{4}{k}y$-4=0.
∴y1+y2=$\frac{4}{k}$,y1y2=-4.∴|y1-y2|=$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\sqrt{\frac{16}{{k}^{2}}+16}$.
∴S△AOB=$\frac{1}{2}×OF×|{y}_{1}-{y}_{2}|$=$\sqrt{\frac{4}{{k}^{2}}+4}$>2.
综上,△AOB面积的最小值为2.
点评 本题考查了抛物线的性质,直线与抛物线的位置关系,属于中档题.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $[{0,\sqrt{2}}]$ | B. | {(-1,1),(1,1)} | C. | {1} | D. | [0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{7}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $±\frac{{\sqrt{3}}}{3}$ | B. | $±\frac{3}{4}$ | C. | ±1 | D. | $±\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
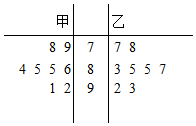 甲、乙两名同学八次数学测试成绩如茎叶图所示,则甲同学成绩的众数与乙同学成绩的中位数依次为( )
甲、乙两名同学八次数学测试成绩如茎叶图所示,则甲同学成绩的众数与乙同学成绩的中位数依次为( )| A. | 85,86 | B. | 85,85 | C. | 86,85 | D. | 86,86 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com