
已知平面上一定点C(-1,0)和一定直线l:x=-4,P为该平面上一动点,作PQ⊥l,垂足为Q,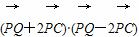 =0.
=0.
(1)问点P在什么曲线上?并求出该曲线方程;
(2)点O是坐标原点,A、B两点在点P的轨迹上,若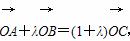 ,求λ的取值范围.
,求λ的取值范围.
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
在平面直角坐标系xOy中,设点F(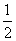 ,0),直线l:x=-
,0),直线l:x=-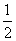 ,点P在直线l上移动,R是线段PF与y轴的交点,RQ⊥FP,PQ⊥l.
,点P在直线l上移动,R是线段PF与y轴的交点,RQ⊥FP,PQ⊥l.
(1)求动点Q的轨迹C的方程;
(2)设圆M过A(1,0),且圆心M在曲线C上,TS是圆M在y轴上截得的弦,当M运动时,弦长|TS|是否为定值?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
过抛物线y2=4x的焦点作一条直线与抛物线相交于A,B两点,它们到直线x=-2的距离之和等于7,则这样的直线( )
A.有且仅有一条 B.有且仅有两条
C.有无穷多条 D.不存在
查看答案和解析>>
科目:高中数学 来源: 题型:
若抛物线y2=4x的焦点为F,过F且斜率为1的直线交抛物线于A、B两点,动点P在曲线y2=-4x(y≥0)上,则△PAB的面积的最小值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
若F1,F2是椭圆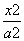 +
+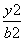 =1(a>2b>0)的两个焦点,分别过F1,F2作倾斜角为45°的两条直线与椭圆相交于四点,以该四点为顶点的四边形和以椭圆的四个顶点为顶点的四边形的面积比等于
=1(a>2b>0)的两个焦点,分别过F1,F2作倾斜角为45°的两条直线与椭圆相交于四点,以该四点为顶点的四边形和以椭圆的四个顶点为顶点的四边形的面积比等于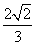 ,则该椭圆的离心率为( )
,则该椭圆的离心率为( )
A.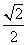 B.
B.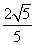
C.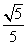 D.
D.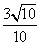
查看答案和解析>>
科目:高中数学 来源: 题型:
已知四棱锥P-ABCD的正视图是一个底边长为4、腰长为3的等腰三角形,如图分别是四棱锥P-ABCD的侧视图和俯视图.
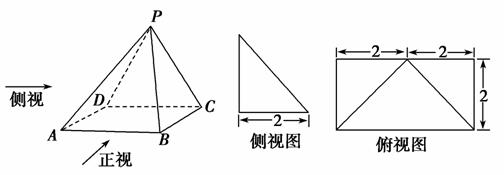
(1)求证:AD⊥PC;
(2)求四棱锥P-ABCD的侧面PAB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com