
分析 解法1 分析法:分析使不等式成立的充分条件,经过分析,使不等式成立的充分条件显然成立,从而证得结论.
解法2 综合法:利用重要不等式 a2d2+b2c2≥2abcd,把(ac+bd)2=a2c2+b2d2+2abcd 放大,即得要证的不等式.
解法3 作差法:把(a2+b2)(c2+d2)-(ac+bd)2 展开化简化成完全平方的形式判断符号,可得其值大于或等于0,从而证得不等式成立.
解答 证明:解法1 (分析法)要证(ac+bd)2≤(a2+b2)(c2+d2),(2分)
即证:a2c2+b2d2+2abcd≤a2c2+a2d2+b2c2+b2d2 ,(4分)
即证:2abcd≤a2d2+b2c2 ,(6分)
即证:0≤a2d2+b2c2-2abcd=(ad+bc)2,(8分)
上式明显成立.(10分) 故(ac+bd)2≤(a2+b2)(c2+d2)(12分)
解法2 (综合法)因为a2d2+b2c2≥2abcd(重要不等式)(3分)
所以(ac+bd)2=a2c2+b2d2+2abcd(6分)≤a2c2+a2d2+b2c2+b2d2(9分)=(a2+b2)(c2+d2)(12分)
解法3 (作差法)因为(a2+b2)(c2+d2)-(ac+bd)2(2分)=(a2c2+a2d2+b2c2+b2d2)-(a2c2+b2d2+2abcd)(5分)
=b2c2+a2d2-2abcd(8分)=(b2c2-a2d2)2≥0(10分)
所以(ac+bd)2≤(a2+b2)(c2+d2). (12分)
点评 本题考查用分析法、综合法、作差比较法证明不等式,式子的变形时解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,3) | B. | [1,3) | C. | [1,3] | D. | (1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
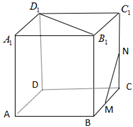 如图,点M,N分别是正方体ABCD-A1B1C1D1的棱BC,CC1的中点,则异面直线B1D1和MN所成的角是( )
如图,点M,N分别是正方体ABCD-A1B1C1D1的棱BC,CC1的中点,则异面直线B1D1和MN所成的角是( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M={3,2},N={(3,2)} | B. | M={3,2},N={2,3} | ||
| C. | M={(x,y)|y=-x+1},N={y|y=1-x} | D. | M={1,2},N={(2,1)} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com