
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() ,图象过点
,图象过点![]() .
.
(1)求![]() 、
、![]() 的值和
的值和![]() 的单调增区间;
的单调增区间;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数
个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数![]() 的图象,若函数
的图象,若函数![]() 在区间
在区间![]() 上有且只有两个不同零点,求实数
上有且只有两个不同零点,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】从某学校高三年级共800名男生中随机抽取50名学生作为样本测量身高.测量发现被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组![]() ;第二组
;第二组![]() ;…;第八组
;…;第八组![]() .下图是按上述分组方法得到的频率分布直方图的一部分.已知第一组与第八组人数相同,第六组与第八组人数之和为第七组的两倍.
.下图是按上述分组方法得到的频率分布直方图的一部分.已知第一组与第八组人数相同,第六组与第八组人数之和为第七组的两倍.
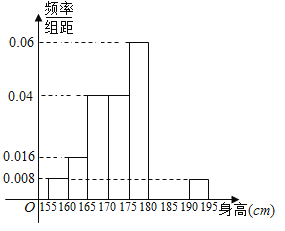
(1)估计这所学校高三年级全体男生身高在180cm以上(含180cm)的人数;
(2)求第六组和第七组的频率并补充完整频率分布直方图.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:x-2y+3=0与直线l2:2x+3y-8=0的交点为M,
(1)求过点M且到点P(0,4)的距离为2的直线l的方程;
(2)求过点M且与直线l3:x+3y+1=0平行的直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() ,
, ![]() .
.
(1)求证:对![]() ,直线
,直线![]() 与圆
与圆![]() 总有两个不同的交点
总有两个不同的交点![]() ;
;
(2)求弦![]() 的中点
的中点![]() 的轨迹方程,并说明其轨迹是什么曲线;
的轨迹方程,并说明其轨迹是什么曲线;
(3)是否存在实数![]() ,使得原
,使得原![]() 上有四点到直线
上有四点到直线![]() 的距离为
的距离为![]() ?若存在,求出
?若存在,求出![]() 的范围;若不存在,说明理由.
的范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,设圆
,设圆![]() 的半径为1, 圆心在
的半径为1, 圆心在![]() 上.
上.

(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线方程;
的切线,求切线方程;
(2)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2012年,在“杂交水稻之父”袁隆平的实验田内种植了![]() ,
,![]() 两个品种的水稻,为了筛选出更优的品种,在
两个品种的水稻,为了筛选出更优的品种,在![]() ,
,![]() 两个品种的实验田中分别抽取7块实验田,如图所示的茎叶图记录了这14块实验田的亩产量(单位:
两个品种的实验田中分别抽取7块实验田,如图所示的茎叶图记录了这14块实验田的亩产量(单位:![]() ),通过茎叶图比较两个品种的均值及方差,并从中挑选一个品种进行以后的推广,有如下结论:①
),通过茎叶图比较两个品种的均值及方差,并从中挑选一个品种进行以后的推广,有如下结论:①![]() 品种水稻的平均产量高于
品种水稻的平均产量高于![]() 品种水稻,推广
品种水稻,推广![]() 品种水稻;②
品种水稻;②![]() 品种水稻的平均产量高于
品种水稻的平均产量高于![]() 品种水稻,推广
品种水稻,推广![]() 品种水稻;③
品种水稻;③![]() 品种水稻比
品种水稻比![]() 品种水稻产量更稳定,推广
品种水稻产量更稳定,推广![]() 品种水稻;④
品种水稻;④![]() 品种水稻比
品种水稻比![]() 品种水稻产量更稳定,推广
品种水稻产量更稳定,推广![]() 品种水稻;其中正确结论的编号为( )
品种水稻;其中正确结论的编号为( )

A.①②B.①③C.②④D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点,过点
两点,过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
![]() 若直线
若直线![]() 垂直平分弦
垂直平分弦![]() ,求实数
,求实数![]() 的值;
的值;
![]() 已知点
已知点![]() ,在直线
,在直线![]() 上(
上(![]() 为圆心),存在定点
为圆心),存在定点![]() (异于点
(异于点![]() ),满足:对于圆
),满足:对于圆![]() 上任一点
上任一点![]() ,都有
,都有![]() 为同一常数,试求所有满足条件的点
为同一常数,试求所有满足条件的点![]() 的坐标及该常数.
的坐标及该常数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com