
分析 ①根据题意,可得y1=y2=0,根据定义直接判断;
②利用定义可得出d(A,B)=|1-x|+|1+x|,利用x的范围去绝对值可得结论;
③利用换元法得出则d(A,B)=3-2sin(θ+$\frac{π}{6}$),进而求出d的范围;
④根据均值定理公式ab≤${(\frac{a+b}{2})}^{2}$,结合定义和距离的内在关系得出结论.
解答 解:①若A,B是x轴上两点,
∴y1=y2=0,则d(A,B)=|x1-x2|,故正确;
②已知点A(1,2),点B在线段x+y=1(x∈[0,1])上,则d(A,B)=|1-x|+|1+x|=2,故正确;
③已知点A(2,1),点B在椭圆$\frac{{x}^{2}}{3}$+y2=1上,
∴设x=$\sqrt{3}$sinθ,则y=cosθ,
则d(A,B)=3-2sin(θ+$\frac{π}{6}$),故d的取值范围是(1,5),故正确;
④若|AB|表示A,B两点间的距离,
设a=|x1-x2|,b=|y1-y2|,
∴ab≤${(\frac{a+b}{2})}^{2}$,d2=a2+b2+2ab,
∴d2-a2-b2=2ab≤${(\frac{d}{2})}^{2}$,
∴|AB|≥$\frac{\sqrt{2}}{2}$d(A,B),故正确.
故答案为:①②③④.
点评 考查了对新定义类型题的理解和利用学过的直接解决问题的能力.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{π}{12}$ | B. | x=$\frac{π}{6}$ | C. | x=-$\frac{π}{6}$ | D. | x=$\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
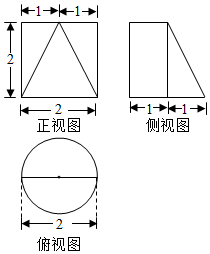
| A. | $\frac{8π}{3}$ | B. | $\frac{4π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1} | B. | {0,1,10} | C. | {1} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,-\frac{1}{8})$ | B. | $(-\frac{1}{8},0)$ | C. | $(0,-\frac{1}{2})$ | D. | $(-\frac{1}{2},0)$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com