考点:平面与平面垂直的判定,棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)由已知得A
1F⊥BB
1,A
1F⊥B
1F,由此能证明平面A
1EF⊥平面BB
1F.
(2)取A
1D
1的中点P,D
1P的中点H,连结DP、EH,则DP∥B
1G,EH∥DP,由此能求出H在A
1D
1上,且HD
1=
A
1D
1时,EH∥平面FGB
1.
(3)由
V四面体EFGB1=
VE-FGB1=VH-FGB1,利用等积法能求出四面体EFGB
1的体积.
解答:
(1)证明:∵长方体AC
1中,BB
1⊥平面A
1B
1C
1D
1,
A
1F?平面A
1B
1C
1D
1,∴A
1F⊥BB
1,
∵长方体AC
1中,AB=2,BC=AA
1=1,
E、F、G分别为棱DD
1、D
1C
1、BC的中点,
∴A
1F⊥B
1F,
∴A
1F⊥平面BB
1F,
又∴A
1F?平面A
1EF,∴平面A
1EF⊥平面BB
1F.
(2)解:取A
1D
1的中点P,D
1P的中点H,
连结DP、EH,则DP∥B
1G,EH∥DP,
∴EH∥B
1G,又B
1G?平面FGB
1,∴EH∥平面FGB
1.
即H在A
1D
1上,且HD
1=
A
1D
1时,EH∥平面FGB
1.
(3)解:∵EH∥平面FGB
1,∴
VE-FGB1=VH-FGB1,
而
VH-FGB1=VG-HFB1=
×1×
S△D1HF,
S△HFB1=
S梯形B1C1D1H-
S△B1C1F-
S△D1HF=
,
∴
V四面体EFGB1=
VE-FGB1=VH-FGB1=
×1×
=
.
点评:本题考查平面与平面垂直的证明,考查满足直线与平面平行的点的确定,考查四面体体积的求法,解题时要认真审题,注意空间思维能力的培养.

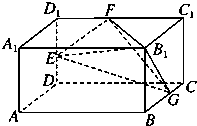 如图,长方体AC1中,AB=2,BC=AA1=1.E、F、G分别为棱DD1、D1C1、BC的中点.
如图,长方体AC1中,AB=2,BC=AA1=1.E、F、G分别为棱DD1、D1C1、BC的中点.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案