练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    用数学归纳法证明1＋2＋3＋…＋n2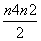＝，则当n＝k＋1时左端应在n＝k的基础上加上(　　)

    A．k2＋1

    B．(k＋1)2

    C.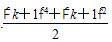

    D．(k2＋1)＋(k2＋2)＋(k2＋3)＋…＋(k＋1)2


    　D

    [解析]　∵当n＝k时，左侧＝1＋2＋3＋…＋k2，

    当n＝k＋1时，

    左侧＝1＋2＋3＋…＋k2＋(k2＋1)＋…＋(k＋1)2，

    ∴当n＝k＋1时，左端应在n＝k的基础上加上

    (k2＋1)＋(k2＋2)＋(k2＋3)＋…＋(k＋1)2.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    如图是计算函数

    y＝的值的程序框图，在①、②、③处应分别填入的是____________________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    观察(x2)′＝2x，(x4)′＝4x3，(cosx)′＝－sinx，由归纳推理可得：若定义在R上的函数f(x)满足f(－x)＝f(x)，记g(x)为f(x)的导函数，则g(－x)＝(　　)

    A．f(x)　　　B．－f(x)　　　C．g(x)　　　D．－g(x)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知椭圆具有性质：若M、N是椭圆C上关于原点对称的两个点，点P是椭圆上任意一点，当直线PM、PN的斜率都存在，并记为kPM、kPN时，那么kPM与kPN之积是与点P的位置无关的定值．试对双曲线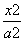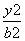－＝1(a>0，b>0)，写出具有类似的性质，并加以证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    用数学归纳法证明“n3＋(n＋1)3＋(n＋2)3(n∈N＋)能被9整除”，要利用归纳假设证n＝k＋1时的情况，只需展开(　　)

    A．(k＋3)3                                                    B．(k＋2)3

    C．(k＋1)3                                                    D．(k＋1)3＋(k＋2)3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    是否存在常数a、b、c使等式12＋22＋32＋…＋n2＋(n－1)2＋…＋22＋12＝an(bn2＋c)对于一切n∈N＋都成立，若存在，求出a、b、c并证明；若不存在，试说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图所示，圆O的直径AB＝6，C为圆周上一点，BC＝3，过C作圆的切线l，求点A到直线l的距离AD.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在直角坐标系xOy中，以原点O为极点，x轴的正半轴为极轴建立极坐标系．曲线C1的参数方程为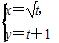(t为参数)，曲线C2的极坐标方程为ρsinθ－ρcosθ＝3，则C1与C2交点在直角坐标系中的坐标为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知直线y＝a交抛物线y＝x2于A、B两点，若该抛物线上存在点C，使得∠ACB为直角，则a的取值范围为________．

    查看答案和解析>>

    同步练习册答案