
是否存在常数a、b、c使等式12+22+32+…+n2+(n-1)2+…+22+12=an(bn2+c)对于一切n∈N+都成立,若存在,求出a、b、c并证明;若不存在,试说明理由.
假设存在a、b、c使12+22+32+…+n2+(n-1)2+…+22+12=an(bn2+c)对于一切n∈N+都成立.
当n=1时,a(b+c)=1;
当n=2时,2a(4b+c)=6;
当n=3时,3a(9b+c)=19.
解方程组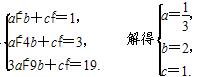
证明如下:
①当n=1时,由以上知存在常数a,b,c使等式成立.
②假设n=k(k∈N+)时等式成立,
即12+22+32+…+k2+(k-1)2+…+22+12
=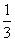 k(2k2+1);
k(2k2+1);
当n=k+1时,
12+22+32+…+k2+(k+1)2+k2+(k-1)2+…+22+12
=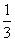 k(2k2+1)+(k+1)2+k2
k(2k2+1)+(k+1)2+k2
=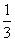 k(2k2+3k+1)+(k+1)2
k(2k2+3k+1)+(k+1)2
=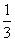 k(2k+1)(k+1)+(k+1)2
k(2k+1)(k+1)+(k+1)2
=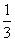 (k+1)(2k2+4k+3)
(k+1)(2k2+4k+3)
=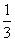 (k+1)[2(k+1)2+1].
(k+1)[2(k+1)2+1].
即n=k+1时,等式成立.
因此存在a=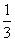 ,b=2,c=1使等式对一切n∈N+都成立.
,b=2,c=1使等式对一切n∈N+都成立.


 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
观察下列事实:|x|+|y|=1的不同整数解(x,y)的个数为4 , |x|+|y|=2的不同整数解(x,y)的个数为8, |x|+|y|=3的不同整数解(x,y)的个数为12,…,则|x|+|y|=20的不同整数解(x,y)的个数为( )
A.76 B.80
C.86 D.92
查看答案和解析>>
科目:高中数学 来源: 题型:
用数学归纳法证明1+2+3+…+n2=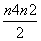 ,则当n=k+1时左端应在n=k的基础上加上( )
,则当n=k+1时左端应在n=k的基础上加上( )
A.k2+1
B.(k+1)2
C.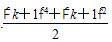
D.(k2+1)+(k2+2)+(k2+3)+…+(k+1)2
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,△ABC为圆的内接三角形,BD为圆的弦,且BD∥AC.过点A作圆的切线与DB的延长线交于点E,AD与BC交于点F.若AB=AC,AE=6,BD=5,则线段CF的长为________.
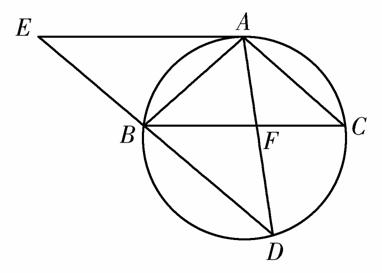
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com