
观察(x2)′=2x,(x4)′=4x3,(cosx)′=-sinx,由归纳推理可得:若定义在R上的函数f(x)满足f(-x)=f(x),记g(x)为f(x)的导函数,则g(-x)=( )
A.f(x) B.-f(x) C.g(x) D.-g(x)
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
读程序回答问题
甲 乙
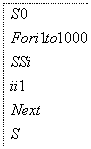

对甲、乙两程序和输出结果判断正确的是( )
A.程序不同,结果不同
B.程序不同,结果相同
C.程序相同,结果不同
D.程序相同,结果相同
查看答案和解析>>
科目:高中数学 来源: 题型:
观察下列事实:|x|+|y|=1的不同整数解(x,y)的个数为4 , |x|+|y|=2的不同整数解(x,y)的个数为8, |x|+|y|=3的不同整数解(x,y)的个数为12,…,则|x|+|y|=20的不同整数解(x,y)的个数为( )
A.76 B.80
C.86 D.92
查看答案和解析>>
科目:高中数学 来源: 题型:
已知x>0,由不等式x+ ≥2
≥2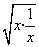 =2,x+
=2,x+ =
=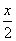 +
+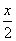 +
+ ≥3
≥3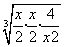 =3,…,我们可以得出推广结论:x+
=3,…,我们可以得出推广结论:x+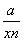 ≥n+1(n∈N+),则a=( )
≥n+1(n∈N+),则a=( )
A.2n B.n2
C.3n D.nn
查看答案和解析>>
科目:高中数学 来源: 题型:
用数学归纳法证明1+2+3+…+n2=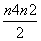 ,则当n=k+1时左端应在n=k的基础上加上( )
,则当n=k+1时左端应在n=k的基础上加上( )
A.k2+1
B.(k+1)2
C.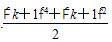
D.(k2+1)+(k2+2)+(k2+3)+…+(k+1)2
查看答案和解析>>
科目:高中数学 来源: 题型:
设集合A={x||x-a|<1,x∈R},B={x||x-b|>2,x∈R}.若A⊆B,则实数a,b必满足( )
A.|a+b|≤3 B.|a+b|≥3
C.|a-b|≤3 D.|a-b|≥3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com