练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，在三棱柱ABC－A1B1C1中，侧棱AA1⊥底面ABC，AB⊥BC，D为AC的中点，AA1＝AB＝2，BC＝3.

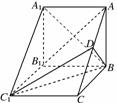
    (1)求证：AB1∥平面BC1D；

    (2)求四棱锥B－AA1C1D的体积．


    解析：　(1)证明：如图，连接B1C，设B1C与BC1相交于点O，连接OD，

    ∵四边形BCC1B1是平行四边形，

    ∴点O为B1C的中点．

    ∵D为AC的中点，∴OD为△AB1C的中位线，

    ∴OD∥AB1，

    ∵OD⊂平面BC1D，AB1⊄平面BC1D，∴AB1∥平面BC1D.

    (2)∵AA1⊥平面ABC，AA1⊂平面AA1C1C，

    ∴平面ABC⊥平面AA1C1C，

    作BE⊥AC，垂足为E，则BE⊥平面AA1C1C.

    在Rt△ABC中，AC＝

    ∴四棱锥B－AA1C1D的体积V＝×(A1C1＋AD)·AA1·BE＝＝3.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


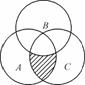
     如图，已知U＝{1，2，3，4，5，6，7，8，9，10}，集合A＝{2，3，4，5，6，8}，B＝{1，3，4，5，7}，C＝{2，4，5，7，8，9}，用列举法写出图中阴影部分表示的集合为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知方程＝1表示焦点在y轴上的椭圆，则实数k的取值范围是(　　)

    A. 　　                   B．(1，＋∞)

    C．(1,2)　　                      D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设正实数x，y，z满足x2－3xy＋4y2－z＝0，则当取得最小值时，x＋2y－z的最大值为(　　)

    A．0　                               B．

    C．2　                               D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}的前n项和为Sn，且Sn＝2an－1；数列{bn}满足bn－1－bn＝bnbn－1(n≥2，n∈N*)，b1＝1.

    (1)求数列{an}，{bn}的通项公式；

    (2)求数列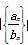的前n项和Tn.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知异面直线a，b分别在平面α，β内，且α∩β＝c，那么直线c一定(　　)

    A．与a，b都相交

    B．只能与a，b中的一条相交

    C．至少与a，b中的一条相交

    D．与a，b都平行

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知四棱锥P－ABCD中，底面ABCD为正方形，PD⊥平面ABCD，EC∥PD，且PD＝2EC.

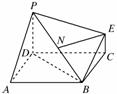
     (1)求证：BE∥平面PDA；

    (2)若N为线段PB的中点，求证：NE⊥平面PDB.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设x，y，z∈R，且满足：x2＋y2＋z2＝1，x＋2y＋3z＝，则x＋y＋z＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，设四棱锥的底面为菱形，且∠，，。

       （Ⅰ）求证：平面平面；

       （Ⅱ）求平面与平面所夹角的余弦值。

    查看答案和解析>>

    同步练习册答案