
已知异面直线a,b分别在平面α,β内,且α∩β=c,那么直线c一定( )
A.与a,b都相交
B.只能与a,b中的一条相交
C.至少与a,b中的一条相交
D.与a,b都平行
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
设全集I=R,已知集合M=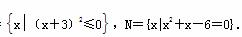 (1) 求(∁IM)∩N;
(1) 求(∁IM)∩N;
(2) 记集合A=(∁IM)∩N,已知集合B={x|a-1≤x≤5-a,a∈R},若B∪A=A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5.若以MF为直径的圆过点(0,2),则C的方程为( )
A.y2=4x或y2=8x B.y2=2x或y2=8x
C.y2=4x或y2=16x D.y2=2x或y2=16x
查看答案和解析>>
科目:高中数学 来源: 题型:
首届世界低碳经济大会在南昌召开,本届大会以“节能减排,绿色生态”为主题.某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本y(元)与月处理量x(吨)之间的函数关系可近似地表示为y=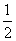 x2-200x+80 000,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
x2-200x+80 000,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2,BC=3.
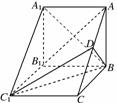
(1)求证:AB1∥平面BC1D;
(2)求四棱锥B-AA1C1D的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
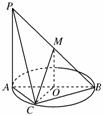
如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M为线段PB的中点.有以下四个命题:
①PA∥平面MOB;②MO∥平面PAC;③OC⊥平面PAC;④平面PAC⊥平面PBC.
其中正确的命题是________(填上所有正确命题的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com