练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设全集I＝R，已知集合M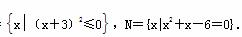＝ (1) 求(∁IM)∩N；

    (2) 记集合A＝(∁IM)∩N，已知集合B＝{x|a－1≤x≤5－a，a∈R}，若B∪A＝A，求实数a的取值范围．


    解：(1) ∵ M＝{x|(x＋3)2≤0}＝{－3}，

    N＝{x|x2＋x－6＝0}＝{－3，2}，

    ∴ ∁IM＝{x|x∈R且x≠－3}，

    ∴ (∁IM)∩N＝{2}．

    (2) A＝(∁IM)∩N＝{2}，

    ∵ A∪B＝A，∴ BA，∴ B＝或B＝{2}，

    当B＝时，a－1>5－a，∴ a>3；

    当B＝{2}时，解得a＝3.

    综上所述，所求a的取值范围为{a|a≥3}．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    为了解某市民众对政府出台楼市限购令的情况，在该市随机抽取了50名市民进行调查，他们月收入(单位：百元)的频数分布及对楼市限购令赞成的人数如下表：

    月收入

    [15,25)

    [25,35)

    [35,45)

    [45,55)

    [55,65)

    [65,75]

    频数

    5

    10

    15

    10

    5

    5

    赞成人数

    4

    8

    12

    5

    2

    1

    将月收入不低于55的人群称为“高收入族”，月收入低于55的人群称为“非高收入族”．

    (1)根据已知条件完成下面的2×2列联表，问能否在犯错误的概率不超过0.01的前提下认为非高收入族赞成楼市限购令？

     

    非高收入族

    高收入族

    合计

    赞成

    不赞成

    合计

    (2)现从月收入在[15,25)的人群中随机抽取两人，求所抽取的两人都赞成楼市限购令的概率．

    附：K2＝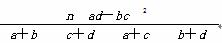

    P(K2≥k0)

    0.05

    0.025

    0.010

    0.005

    k0

    3.841

    5.024

    6.635

    7.879

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    集合A＝{x|－2≤x≤5}，集合B＝{x|m＋1≤x≤2m－1}．　

    (1) 若BA，求实数m的取值范围；

    (2) 当x∈R时，没有元素x使x∈A与x∈B同时成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若全集U＝{1，2，3，4，5，6}，M∩N＝N，N＝{1，4}，试求满足条件的集合M的个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     如图，已知U＝{1，2，3，4，5，6，7，8，9，10}，集合A＝{2，3，4，5，6，8}，B＝{1，3，4，5，7}，C＝{2，4，5，7，8，9}，用列举法写出图中阴影部分表示的集合为________．

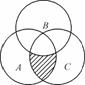
    查看答案和解析>>

    科目：高中数学 来源： 题型：


    写出命题“若x＋y＝5，则x＝3且y＝2”的逆命题、否命题、逆否命题，并判断它们的真假．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    命题“所有不能被2整除的整数都是奇数”的否定是________________________________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的列联表：

     

    男

    女

    总计

    爱好

    40

    20

    60

    不爱好

    20

    30

    50

    总计

    60

    50

    110

    由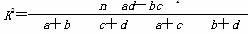算得，

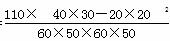    K2＝≈7.8.

    附表：

    P(K2≥k)

    0.050

    0.010

    0.001

    k

    3.841

    6.635

    10.828

    参照附表，得到的正确结论是(　　)

    A．有99%以上的把握认为“爱好该项运动与性别有关”

    B．有99%以上的把握认为“爱好该项运动与性别无关”

    C．在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关”

    D．在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别无关”

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知异面直线a，b分别在平面α，β内，且α∩β＝c，那么直线c一定(　　)

    A．与a，b都相交

    B．只能与a，b中的一条相交

    C．至少与a，b中的一条相交

    D．与a，b都平行

    查看答案和解析>>

    同步练习册答案