
(本题满分15分)在数列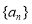 中,
中,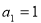 ,当
,当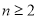 时,满足
时,满足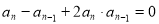 .
.
(Ⅰ)求证:数列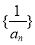 是等差数列,并求数列
是等差数列,并求数列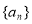 的通项公式;
的通项公式;
(Ⅱ)令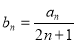 ,数列
,数列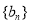 的前
的前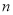 项和为
项和为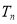 ,求使得
,求使得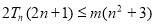 对所有
对所有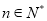 都成立的实数
都成立的实数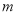 的取值范围.
的取值范围.
(Ⅰ)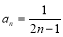 ;(Ⅱ)满足题意的实数
;(Ⅱ)满足题意的实数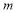 的取值范围为
的取值范围为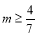 .
.
【解析】
试题分析:(Ⅰ)求证:数列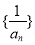 是等差数列,只需证明
是等差数列,只需证明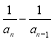 等于一个与
等于一个与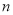 无关的常数,由已知,
无关的常数,由已知,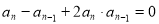 ,只需将式子整理得,
,只需将式子整理得,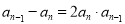 ,两边同除以
,两边同除以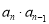 即可,求数列
即可,求数列 的通项公式,因为数列
的通项公式,因为数列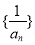 是以
是以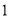 为首项,
为首项,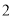 为公差的等差数列,可写出数列
为公差的等差数列,可写出数列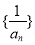 的通项公式,从而可得数列
的通项公式,从而可得数列 的通项公式; (Ⅱ)求使得
的通项公式; (Ⅱ)求使得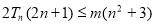 对所有
对所有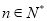 都成立的实数
都成立的实数 的取值范围,将式子整理为
的取值范围,将式子整理为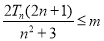 ,只需求出
,只需求出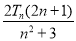 的最大值,须求出
的最大值,须求出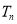 的解析式,首先求出数列
的解析式,首先求出数列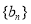 的通项公式,由
的通项公式,由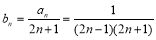 ,可用拆项相消法求得
,可用拆项相消法求得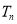 的解析式,进而可得实数
的解析式,进而可得实数 的取值范围.
的取值范围.
试题解析:(Ⅰ),两边同除以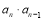 得
得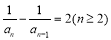 ,即数列
,即数列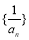 是等差数列,首项
是等差数列,首项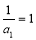 ,公差
,公差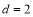
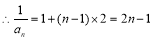
 ;
;
(Ⅱ)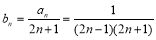
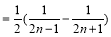
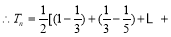
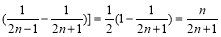
由题意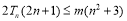 即
即 对于所有
对于所有 都成立,
都成立,
设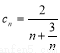 即
即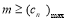
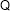 函数
函数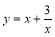 在
在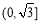 上是减函数,在
上是减函数,在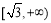 上是增函数,故数列
上是增函数,故数列 从第二项起递减,而
从第二项起递减,而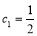 ,
,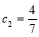
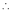 满足题意的实数
满足题意的实数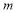 的取值范围为
的取值范围为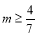 .
.
考点:等差数列的判断,求数列的通项公式.


科目:高中数学 来源:2014-2015学年江苏省等五校高三12月第一次联考理科数学试卷(解析版) 题型:解答题
(本小题满分10分)袋中装有大小相同的黑球和白球共9个,从中任取2个都是白球的概率为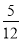 .现甲、乙两人从袋中轮流摸球,甲先取,乙后取,然后甲再取 ,每次摸取1个球,取出的球不放回,直到其中有一人取到白球时终止.用X表示取球终止时取球的总次数.
.现甲、乙两人从袋中轮流摸球,甲先取,乙后取,然后甲再取 ,每次摸取1个球,取出的球不放回,直到其中有一人取到白球时终止.用X表示取球终止时取球的总次数.
(1)求袋中原有白球的个数;
(2)求随机变量X的概率分布及数学期望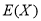 .
.
查看答案和解析>>
科目:高中数学 来源:2015届江苏教育学院附属高中高三上学期期中理科数学试卷(解析版) 题型:填空题
定义在(-1,1)上的函数f(x)=-3x+sinx,如果f(1-a)+f(1-a2)>0,则实数 的取值范围为 .
的取值范围为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省嘉兴市高三新高考单科综合调研三文科数学试卷(解析版) 题型:填空题
已知平行四边形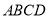 中,
中,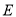 为
为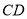 的中点,
的中点,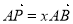 ,
,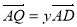 ,其中
,其中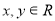 ,且均不为0,若
,且均不为0,若 ,则
,则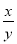 = .
= .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省嘉兴市高三新高考单科综合调研三文科数学试卷(解析版) 题型:选择题
椭圆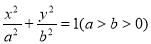 上一点
上一点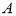 关于原点的对称点为
关于原点的对称点为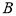 ,
,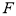 为其左焦点,若
为其左焦点,若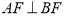 ,设
,设 ,则该椭圆的离心率为 ( )
,则该椭圆的离心率为 ( )
A.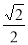 B.
B.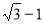 C.
C.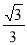 D.
D.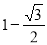
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省高三12月月考理科数学试卷(解析版) 题型:填空题
已知下列五个命题:
①若一个圆锥的底面半径缩小到原来的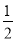 ,其体积缩小到原来的
,其体积缩小到原来的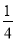 ;
;
②若两组数据的中位数相等,则它们的平均数也相等;
③直线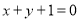 与圆
与圆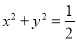 相切;
相切;
④“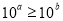 ”是“
”是“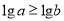 ”的充分不必要条件.
”的充分不必要条件.
⑤过M(2,0)的直线l与椭圆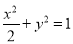 交于P1P2两点,线段P1P2中点为P,设直线l的斜率为k1(k1≠0),直线OP的斜率为k2,则k1k2等于-
交于P1P2两点,线段P1P2中点为P,设直线l的斜率为k1(k1≠0),直线OP的斜率为k2,则k1k2等于-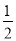
其中真命题的序号是:____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com