分析:(1)根据反比例函数y=
的图象C是以x轴与y轴为渐近线的等轴双曲线,即可求双曲线C的顶点坐标与焦点坐标;
(2)先把直线l的方程以及A、B两点的坐标设出来,利用
=λ
1=λ
2,找到λ
1和λ
2与A、B两点的坐标和直线l的斜率的关系,再利用A、B两点是直线和双曲线的交点以及λ
1+λ
2=-8,求出直线l的斜率k进而求出Q点的坐标.
解答:
解:(1)由题意得:顶点:(-1,-1)、(1,1),---------------------------------(2分)
焦点:(-
,-
)、(
,
)为焦点.--------------------------------------(4分)
(2)①直线l斜率不存在或为0时显然不满足条件;
设直线l:y=kx+4(k≠0),A(x
1,y
1),B(x
2,y
2),M(x,y),---------------------(1分)
将y=kx+4代入y=
,得kx
2+4x-1=0,--------------------------------------(1分)
△=16+4k>0,∴k>-4,--------------------------------------(1分)
x
1+x
2=-
,x
1x
2=-
,-------------------------------(1分)
∴x=-
,y=2,--------------------------------------(1分)
∵k>-4,∴x∈(-∞,0)∪(
,+∞),--------------------------------------(2分)
∴A、B中点M的轨迹方程为y=2(x∈(-∞,0)∪(
,+∞),------------(1分)
②直线l斜率不存在或为0时显然不满足条件;-------------------------------------(1分)
设直线l:y=kx+4(k≠0),A(x
1,y
1),B(x
2,y
2),则Q(-
,0)-----------------------(1分)
将y=kx+4代入y=
,得kx
2+4x-1=0,--------------------------------------(1分)
∵
=λ
1=λ
2,
∴(-
,-4)=λ
1(x
1+
,y
1)=λ
2(x
2+
,y
2),-----------(1分)
∴λ
1+λ
2=
+=-8,即2k
2x
1x
2+7k(x
1+x
2)+24=0,
解得k=-2,--------------------------------------(2分)
∴Q(2,0).--------------------------------------(1分)



 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案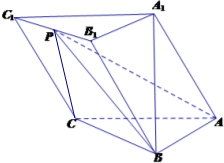 如图,在三棱柱ABC-A1B1C1中,AB⊥AC,顶点A1在底面ABC上的射影恰为点B,且AB=AC=A1B=2.
如图,在三棱柱ABC-A1B1C1中,AB⊥AC,顶点A1在底面ABC上的射影恰为点B,且AB=AC=A1B=2. 如图,AB是圆O的直径,点C是圆O上异于A、B的点,直线PC⊥平面ABC,E,F分别为PA,PC的中点.
如图,AB是圆O的直径,点C是圆O上异于A、B的点,直线PC⊥平面ABC,E,F分别为PA,PC的中点.