考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(I)由已知可得A1B⊥面ABC,进而A1B⊥AC,结合AB⊥AC和线面垂直的判定定理可得AC⊥面AB1B,再由面面垂直的判定定理得到平面A1AC⊥平面AB1B;
(Ⅱ)若点P为B1C1的中点,点P到平面AA1B1B距离h2等于点C1到平面AA1B1B的距离的一半,求出底面积,代入棱锥体积公式,可得答案.
解答:

证明:(Ⅰ)∵顶点A
1在底面ABC上的射影恰为点B,
∴A
1B⊥面ABC,
又∵AC?面ABC,
∴A
1B⊥AC,------(2分)
又AB⊥AC,AB∩A
1B=B,AB,A
1B?面AB
1B,
∴AC⊥面AB
1B,------(3分)
∵AC?面A
1AC,
∴平面A
1AC⊥平面AB
1B;------(5分)
(Ⅱ)在三棱锥P-ABC中,因为AB⊥AC,
所以底面ABC是等腰直角三角形,
又因为点P到底面的距离h=A
1B=2,
所以
VP-ABC=S△ABC•h=•AC•AB•h=.------(6分)
由(Ⅰ)可知AC⊥面AB
1B,
因为点P在B
1C
1的中点,
所以点P到平面AA
1B
1B距离h
2等于点C
1到平面AA
1B
1B的距离的一半,即h
2=1.------(8分)
VP-AA1B1B=S四边形AA1B1B•h2=AB•A1B•h2=•2•2•1=,------(10分)
所以三棱锥P-ABC与四棱锥P-AA
1B
1A
1的体积之比为1:1.------(12分)
点评:本题考查的知识点是棱锥的体积,平面与平面垂直的判定,直线与平面垂直的判定与性质,难度中档.

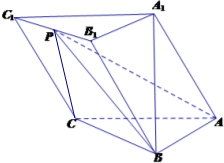 如图,在三棱柱ABC-A1B1C1中,AB⊥AC,顶点A1在底面ABC上的射影恰为点B,且AB=AC=A1B=2.
如图,在三棱柱ABC-A1B1C1中,AB⊥AC,顶点A1在底面ABC上的射影恰为点B,且AB=AC=A1B=2. 证明:(Ⅰ)∵顶点A1在底面ABC上的射影恰为点B,
证明:(Ⅰ)∵顶点A1在底面ABC上的射影恰为点B,

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案