
【题目】如图在棱长均为2的正四棱锥P﹣ABCD中,点E为PC中点,则下列命题正确的是( ) 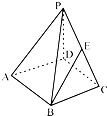
A.BE平行面PAD,且直线BE到面PAD距离为 ![]()
B.BE平行面PAD,且直线BE到面PAD距离为 ![]()
C.BE不平行面PAD,且BE与平面PAD所成角大于 ![]()
D.BE不平行面PAD,且BE与面PAD所成角小于 ![]()
【答案】D
【解析】解:连接AC,BD,交点为O,以O为坐标原点,OC,OD,OP方向分别x,y,z轴正方向建立空间坐标系,
由正四棱锥P﹣ABCD的棱长均为2,点E为PC的中点,
则O(0,0,0),A(﹣ ![]() ,0,0),B(0,﹣
,0,0),B(0,﹣ ![]() ,0),
,0),
C( ![]() ,0,0),D(0,
,0,0),D(0, ![]() ,0),
,0),
P(0,0, ![]() ),E(
),E( ![]() ,0,
,0, ![]() ),
),
则 ![]() =(
=( ![]() ,
, ![]() ,
, ![]() ),
), ![]() =(﹣
=(﹣ ![]() ,0,﹣
,0,﹣ ![]() ),
),![]() =(0,
=(0, ![]() ,﹣
,﹣ ![]() ),
),
设 ![]() =(x,y,z)是平面PAD的一个法向量,
=(x,y,z)是平面PAD的一个法向量,
则 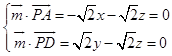 ,
,
取x=1,得 ![]() =(1,﹣1,﹣1),
=(1,﹣1,﹣1),
设BE与平面PAD所成的角为θ,
则sinθ=|cos< ![]() ,
, ![]() >|=|
>|=| ![]() |=
|= ![]() <
< ![]() ,
,
故BE与平面PAD不平行,且BE与平面PAD所成的角小于30°.
由此排除选项A,B,C.
故选:D.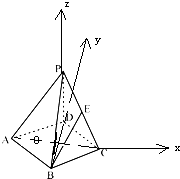
【考点精析】认真审题,首先需要了解空间中直线与平面之间的位置关系(直线在平面内—有无数个公共点;直线与平面相交—有且只有一个公共点;直线在平面平行—没有公共点).


科目:高中数学 来源: 题型:
【题目】张老师开车上班,有路线①与路线②两条路线可供选择. 路线①:沿途有![]() 两处独立运行的交通信号灯,且两处遇到绿灯的概率依次为
两处独立运行的交通信号灯,且两处遇到绿灯的概率依次为![]() ,若
,若![]() 处遇红灯或黄灯,则导致延误时间2分钟;若
处遇红灯或黄灯,则导致延误时间2分钟;若![]() 处遇红灯或黄灯,则导致延误时间3分钟;若两处都遇绿灯,则全程所花时间为20分钟.
处遇红灯或黄灯,则导致延误时间3分钟;若两处都遇绿灯,则全程所花时间为20分钟.
路线②:沿途有![]() 两处独立运行的交通信号灯,且两处遇到绿灯的概率依次为
两处独立运行的交通信号灯,且两处遇到绿灯的概率依次为![]() ,若
,若![]() 处遇红灯或黄灯,则导致延误时间8分钟;若
处遇红灯或黄灯,则导致延误时间8分钟;若![]() 处遇红灯或黄灯,则导致延误时间5分钟;若两处都遇绿灯,则全程所花时间为15分钟.
处遇红灯或黄灯,则导致延误时间5分钟;若两处都遇绿灯,则全程所花时间为15分钟.
(1)若张老师选择路线①,求他20分钟能到校的概率;
(2)为使张老师日常上班途中所花时间较少,你建议张老师选择哪条路线?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据下列算法语句,将输出的A值依次记为a1 , a2 , …,an , …,a2015;已知函数f(x)=a2sin(ωx+φ)(ω>0,|φ|< ![]() )的最小正周期是a1 , 且函数y=f(x)的图象关于直线x=
)的最小正周期是a1 , 且函数y=f(x)的图象关于直线x= ![]() 对称.
对称.
(Ⅰ)求函数y=f(x)表达式;
(Ⅱ)已知△ABC中三边a,b,c对应角A,B,C,a=4,b=4 ![]() ,∠A=30°,求f(B).
,∠A=30°,求f(B).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)= (x∈R).
(x∈R).
(1)求函数f(x)的最小值;
(2)已知m∈R,命题p:关于x的不等式f(x)≥m2+2m-2对任意x∈R恒成立;q:函数y=(m2-1)x是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的离心率为
的离心率为![]() ,过左焦点
,过左焦点![]() 且斜率为
且斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() ,
, ![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点.
两点.
(I)求椭圆![]() 的方程.
的方程.
(II)求证:点![]() 在直线
在直线![]() 上.
上.
(III)是否存在实数![]() ,使得
,使得![]() 的面积是
的面积是![]() 面积的
面积的![]() 倍?若存在,求出
倍?若存在,求出![]() 的值.若不存在,说明理由.
的值.若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=2x﹣1.
(1)求f(3)+f(﹣1);
(2)求f(x)的解析式;
(3)若x∈A,f(x)∈[﹣7,3],求区间A.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com