
| A. | ①②③ | B. | ②③ | C. | ① | D. | ①② |
分析 命题①直接由替代的定义得出为真命题;命题②根据替代的定义,|f(x)-g(x)|≤1在[1,e]上恒成立,根据导数判断函数lnx-x+b在[1,e]上的单调性,根据单调性即可求出函数lnx-x+b的值域,该值域应为区间[-1,1]的子集,从而可得出b的取值范围,从而判断该命题的正误;命题③可先找出一个D1∩D2区间,可以在此区间找到一个x使对任意a|f(x)-g(x)|>1,从而便可判断出该命题错误,这样便可最后找出所有的真命题.
解答 解:在①中,∵f(x)=x2+1,g(x)=x2+$\frac{1}{2}$,
∴对任意x∈(-∞,+∞),都有|f(x)-g(x)|=|1-$\frac{1}{2}$|=$\frac{1}{2}$≤1成立,
∴f(x)=x2+1在区间(-∞,+∞)上可被g(x)=x2+$\frac{1}{2}$替代,故①正确;
在②中,由题意知:|f(x)-g(x)|=|lnx-x+b|≤1在x∈[1,e]上恒成立;设h(x)=lnx-x+b,则h′(x)=$\frac{1-x}{x}$,
∵x∈[1,e],∴h′(x)≤0,∴h(x)在[1,e]上单调递减,
h(1)=b-1,h(e)=1-e+b,
1-e+b≤h(x)≤b-1,又-1≤h(x)≤1,
∴$\left\{\begin{array}{l}{1-e+b≥-1}\\{b-1≤1}\end{array}\right.$,解得e-2≤b≤2,故②错误;
在③中,若a>0,解ax2+x>0,得x<-$\frac{1}{a}$或x>0,
可取D1=(0,+∞),D2=R,∴D1∩D2=(0,+∞),
可取x=π,则|f(x)-g(x)|=aπ2+π,
∴不存在实数a(a>0),使得f(x)在区间D1∩D2 上被g(x)替代;
若a<0,解ax2+x>0得,x<0,或x>-$\frac{1}{a}$,
∴可取D1=(-∞,0),D2=R,∴D1∩D2=(-∞,0),
取x=-π,则|f(-π)-g(-π)|=|aπ2-π|>1,
∴不存在实数a(a<0),使得f(x)在区间D1∩D2 上被g(x)替代.
综上得,不存在实数a(a≠0),使得f(x)在区间D1∩D2 上被g(x)替代,故③错误.
故选:C.
点评 考查对替代定义的理解,根据函数导数判断函数单调性、求函数在闭区间上最值的方法,以及根据对数的真数大于0求函数定义域的方法,解一元二次不等式,在说明f(x)不能被g(x)替代的举反例即可.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
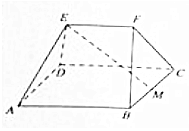 如图,在多面体ABCDEF中,四边形ABCD为边长为4的正方形,M是BC的中点,EF∥平面ABCD,且EF=2,AE=DE=BF=CF=$2\sqrt{2}$.
如图,在多面体ABCDEF中,四边形ABCD为边长为4的正方形,M是BC的中点,EF∥平面ABCD,且EF=2,AE=DE=BF=CF=$2\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
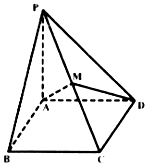 已知四棱锥P-ABCD中,底面为矩形,PA⊥底面ABCD,PA=BC=1,AB=2,M为PC中点.
已知四棱锥P-ABCD中,底面为矩形,PA⊥底面ABCD,PA=BC=1,AB=2,M为PC中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com