
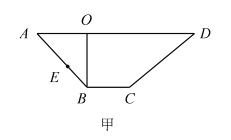
،¾جâؤ؟،؟ؤ³ہدت¦تات،¼¶؟خجâ×éµؤ³ةش±£¬ض÷زھرذ¾؟؟خجأ½جر§ؤ؟±ê´ï³ة¶ب£¬خھ·½±مرذ¾؟£¬´ستµرé°àضذثو»ْ³éب،30´خµؤثوجأ²âتش³ة¼¨½ّذذت¾ف·ضخِ![]() زرضھر§ةْ¼×µؤ30´خثوجأ²âتش³ة¼¨بçدآ
زرضھر§ةْ¼×µؤ30´خثوجأ²âتش³ة¼¨بçدآ![]() آْ·ضخھ100·ض
آْ·ضخھ100·ض![]() £؛
£؛

![]() °رر§ةْ¼×µؤ³ة¼¨°´
°رر§ةْ¼×µؤ³ة¼¨°´![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() ·ض³ة6×飬ءذ³ِئµآت·ض²¼±ي£¬²¢»³ِئµآت·ض²¼ض±·½ح¼£»
·ض³ة6×飬ءذ³ِئµآت·ض²¼±ي£¬²¢»³ِئµآت·ض²¼ض±·½ح¼£»
![]() ¹و¶¨ثوجأ²âتش³ة¼¨80·ضزشةد
¹و¶¨ثوجأ²âتش³ة¼¨80·ضزشةد![]() ؛¬80·ض
؛¬80·ض![]() خھسإذم£¬خھ°ïضْر§ةْ¼×جل¸ك³ة¼¨£¬ر،ب،ر§ةْزز£¬¶ش¼×سëززµؤثوجأ²âتش³ة¼¨½ّذذ¶ش±ب·ضخِ£¬¼×سëزز²âتش³ة¼¨تا·ٌخھسإذمد໥¶ہء¢
خھسإذم£¬خھ°ïضْر§ةْ¼×جل¸ك³ة¼¨£¬ر،ب،ر§ةْزز£¬¶ش¼×سëززµؤثوجأ²âتش³ة¼¨½ّذذ¶ش±ب·ضخِ£¬¼×سëزز²âتش³ة¼¨تا·ٌخھسإذمد໥¶ہء¢![]() زرضھ¼×³ة¼¨سإذمµؤ¸إآتخھ
زرضھ¼×³ة¼¨سإذمµؤ¸إآتخھ![]() زشئµآت¹ہ¼ئ¸إآت
زشئµآت¹ہ¼ئ¸إآت![]() £¬زز³ة¼¨سإذمµؤ¸إآتخھ
£¬زز³ة¼¨سإذمµؤ¸إآتخھ![]() £¬بô
£¬بô![]() £¬شٍ´ث¶بثتت؛دخھر§د°ةد»¥°ï»¥ضْµؤ،°¶ش×س،±
£¬شٍ´ث¶بثتت؛دخھر§د°ةد»¥°ï»¥ضْµؤ،°¶ش×س،±![]() شعز»´خثوجأ²âتشضذ£¬¼ا
شعز»´خثوجأ²âتشضذ£¬¼ا![]() خھء½بثضذ»ٌµأسإذمµؤبثت£¬زرضھ
خھء½بثضذ»ٌµأسإذمµؤبثت£¬زرضھ![]() £¬خت¶بثتا·ٌتت؛د½لخھ،°¶ش×س،±£؟
£¬خت¶بثتا·ٌتت؛د½لخھ،°¶ش×س،±£؟
،¾´ً°¸،؟£¨1£©ض±·½ح¼¼û½âخِ£»£¨2£©تا.
،¾½âخِ،؟
![]() ¸ù¾فجâزâءذ³ِئµآت·ض²¼±ي£¬»³ِئµآت·ض²¼ض±·½ح¼¼´؟ة£»
¸ù¾فجâزâءذ³ِئµآت·ض²¼±ي£¬»³ِئµآت·ض²¼ض±·½ح¼¼´؟ة£»
![]() سةجâزâضھثو»ْ±نء؟Xµؤثùسذ؟ةؤـب،ضµ£¬¼ئثم¶شس¦µؤ¸إآتضµ£¬ذ´³ِ·ض²¼ءذ£¬شظ¼ئثمتر§ئعحûضµ£¬اَ³ِ
سةجâزâضھثو»ْ±نء؟Xµؤثùسذ؟ةؤـب،ضµ£¬¼ئثم¶شس¦µؤ¸إآتضµ£¬ذ´³ِ·ض²¼ءذ£¬شظ¼ئثمتر§ئعحûضµ£¬اَ³ِ![]() زش¼°
زش¼°![]() µؤضµ£¬سة´ثµأ³ِ½لآغ£®
µؤضµ£¬سة´ثµأ³ِ½لآغ£®
![]() ¸ù¾ف³ة¼¨·ض×飬ءذ³ِئµآت·ض²¼±يبçدآ£¬
¸ù¾ف³ة¼¨·ض×飬ءذ³ِئµآت·ض²¼±يبçدآ£¬
·ض×é | ئµتہغ¼ئ | ئµت | ئµآت | ئµآت |
|
| 3 | | |
|
| 3 | | |
|
| 9 | | |
|
| 6 | | |
|
| 6 | | |
|
| 3 | | |
؛د¼ئ | 30 | 1 |
»³ِئµآت·ض²¼ض±·½ح¼بçح¼ثùت¾£»

![]() سة
سة![]() ضھ
ضھ![]() £¬ثو»ْ±نء؟Xµؤثùسذ؟ةؤـب،ضµ·ض±ًخھ0£¬1£¬2£»
£¬ثو»ْ±نء؟Xµؤثùسذ؟ةؤـب،ضµ·ض±ًخھ0£¬1£¬2£»
µ±![]() ت±£¬
ت±£¬![]() £¬
£¬
µ±![]() ت±£¬
ت±£¬![]() £¬
£¬
µ±![]() ت±£¬
ت±£¬![]() £»
£»
ثùزشXµؤ·ض²¼ءذخھ£»
X | 0 | 1 | 2 |
P | | | |
ثùزشXµؤتر§ئعحûخھ![]() £¬
£¬
½âµأ![]() £»
£»
ثùزش![]() £¬
£¬
ثùزشر§ةْ¼×سëر§ةْززتت؛د½لخھ،°¶ش×س،±£®


 ½ج²ؤب«½â×ض´ت¾نئھدµءذ´ً°¸
½ج²ؤب«½â×ض´ت¾نئھدµءذ´ً°¸
| ؤ꼶 | ¸كضذ؟خ³ج | ؤ꼶 | ³ُضذ؟خ³ج |
| ¸كز» | ¸كز»أâ·ر؟خ³جحئ¼ِ£، | ³ُز» | ³ُز»أâ·ر؟خ³جحئ¼ِ£، |
| ¸ك¶ | ¸ك¶أâ·ر؟خ³جحئ¼ِ£، | ³ُ¶ | ³ُ¶أâ·ر؟خ³جحئ¼ِ£، |
| ¸كب | ¸كبأâ·ر؟خ³جحئ¼ِ£، | ³ُب | ³ُبأâ·ر؟خ³جحئ¼ِ£، |
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟شعض±½ا×ّ±êدµ![]() ضذ£¬ض±دك
ضذ£¬ض±دك![]() µؤ²خت·½³جخھ
µؤ²خت·½³جخھ![]() £¨
£¨![]() خھ²خت£©.زش×ّ±êشµمخھ¼«µم£¬
خھ²خت£©.زش×ّ±êشµمخھ¼«µم£¬![]() ضلص°ëضلخھ¼«ضل½¨ء¢¼«×ّ±êدµ£¬اْدك
ضلص°ëضلخھ¼«ضل½¨ء¢¼«×ّ±êدµ£¬اْدك![]() µؤ¼«×ّ±ê·½³جخھ
µؤ¼«×ّ±ê·½³جخھ![]() .
.
£¨¢ٌ£©اَاْدك![]() µؤض±½ا×ّ±ê·½³ج£¬²¢ثµأ÷ثüخھ؛خضضاْدك£»
µؤض±½ا×ّ±ê·½³ج£¬²¢ثµأ÷ثüخھ؛خضضاْدك£»
£¨¢ٍ£©ةèµم![]() µؤ×ّ±êخھ
µؤ×ّ±êخھ![]() £¬ض±دك
£¬ض±دك![]() ½»اْدك
½»اْدك![]() سع
سع![]() £¬
£¬![]() ء½µم£¬اَ
ء½µم£¬اَ![]() µؤب،ضµ·¶خ§.
µؤب،ضµ·¶خ§.
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼¼×ثùت¾£¬ ![]() تاجفذخ
تاجفذخ![]() µؤ¸ك£¬
µؤ¸ك£¬ ![]() £¬
£¬ ![]() £¬
£¬ ![]() £¬دض½«جفذخ
£¬دض½«جفذخ![]() رط
رط![]() صغئًبçح¼ززثùت¾µؤثؤہâ׶
صغئًبçح¼ززثùت¾µؤثؤہâ׶![]() £¬ت¹µأ
£¬ت¹µأ![]() £¬µم
£¬µم![]() تادك¶خ
تادك¶خ![]() ةدز»¶¯µم.
ةدز»¶¯µم.
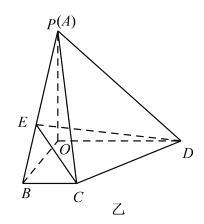
£¨1£©ض¤أ÷£؛ ![]() ؛ح
؛ح![]() ²»؟ةؤـ´¹ض±£»
²»؟ةؤـ´¹ض±£»
£¨2£©µ±![]() ت±£¬اَ
ت±£¬اَ![]() سëئ½أو
سëئ½أو![]() ثù³ة½اµؤصدزضµ.
ثù³ة½اµؤصدزضµ.
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬ةèحضش²![]() £؛
£؛ ![]() £¬³¤ضلµؤسز¶ثµمسëإ×خïدك
£¬³¤ضلµؤسز¶ثµمسëإ×خïدك![]() £؛
£؛ ![]() µؤ½¹µم
µؤ½¹µم![]() ضط؛د£¬ازحضش²
ضط؛د£¬ازحضش²![]() µؤہëذؤآتتا
µؤہëذؤآتتا![]() £®
£®
£¨¢ٌ£©اَحضش²![]() µؤ±ê×¼·½³ج£»
µؤ±ê×¼·½³ج£»
£¨¢ٍ£©¹![]() ×÷ض±دك
×÷ض±دك![]() ½»إ×خïدك
½»إ×خïدك![]() سع
سع![]() £¬
£¬ ![]() ء½µم£¬¹
ء½µم£¬¹![]() ازسëض±دك
ازسëض±دك![]() ´¹ض±µؤض±دك½»حضش²
´¹ض±µؤض±دك½»حضش²![]() سعءيز»µم
سعءيز»µم![]() £¬اَ
£¬اَ![]() أو»µؤ×îذ،ضµ£¬زش¼°ب،µ½×îذ،ضµت±ض±دك
أو»µؤ×îذ،ضµ£¬زش¼°ب،µ½×îذ،ضµت±ض±دك![]() µؤ·½³ج£®
µؤ·½³ج£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬زرضھ¹µم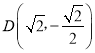 µؤحضش²
µؤحضش²![]() µؤہëذؤآتخھ
µؤہëذؤآتخھ![]() £¬×َ¶¥µم؛حةد¶¥µم·ض±ًخھA£¬B£®
£¬×َ¶¥µم؛حةد¶¥µم·ض±ًخھA£¬B£®
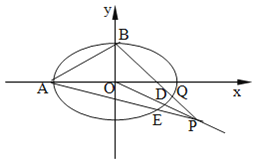
£¨1£©اَحضش²µؤ±ê×¼·½³ج£»
£¨2£©بôPخھدك¶خODرس³¤دكةدز»µم£¬ض±دكPA½»حضش²سعءيز»µمE£¬ض±دكPB½»حضش²سعءيز»µمQ£®
¢ظاَض±دكPAسëPBµؤذ±آتض®»£»
¢عإذ¶دض±دكABسëEQتا·ٌئ½ذذ£؟²¢ثµأ÷ہيسة£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟½«؛¯ت![]() µؤح¼دٌدٍ×َئ½زئ
µؤح¼دٌدٍ×َئ½زئ![]() ¸ِµ¥خ»؛َµأµ½؛¯ت
¸ِµ¥خ»؛َµأµ½؛¯ت![]() µؤح¼دٌ£¬از؛¯ت
µؤح¼دٌ£¬از؛¯ت![]() آْ×م
آْ×م![]() £¬شٍدآءذأüجâضذصب·µؤتا£¨£©
£¬شٍدآءذأüجâضذصب·µؤتا£¨£©
A. ؛¯ت![]() ح¼دٌµؤء½جُدàءع¶ش³ئضلض®¼نµؤ¾àہëخھ
ح¼دٌµؤء½جُدàءع¶ش³ئضلض®¼نµؤ¾àہëخھ![]()
B. ؛¯ت![]() ح¼دٌ¹طسعµم
ح¼دٌ¹طسعµم![]() ¶ش³ئ
¶ش³ئ
C. ؛¯ت![]() ح¼دٌ¹طسعض±دك
ح¼دٌ¹طسعض±دك![]() ¶ش³ئ
¶ش³ئ
D. ؛¯ت![]() شعاّ¼ن
شعاّ¼ن![]() ؤعخھµ¥µ÷µف¼ُ؛¯ت
ؤعخھµ¥µ÷µف¼ُ؛¯ت
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟خزأاضھµہ£¬µطاٍةدµؤث®×تش´سذدق£¬°®»¤µطاٍ،¢½عش¼سأث®تاخزأاأ؟¸ِبثµؤزهخٌ؛حشًبخ.ؤ³تذص¸®خھءث¶ش×شہ´ث®µؤت¹سأ½ّذذ؟ئر§¹ـہي£¬½عش¼ث®×تش´£¬¼ئ»®ب·¶¨ز»¸ِ¼زح¥ؤêسأث®ء؟µؤ±ê×¼£¬خھ´ث£¬¶شب«تذ¼زح¥بص³£سأث®µؤاé؟ِ½ّذذ³éرùµ÷²é£¬²¢»ٌµأءث![]() ¸ِ¼زح¥ؤ³ؤêµؤسأث®ء؟£¨µ¥خ»£؛ء¢·½أ×£©£¬ح³¼ئ½ل¹ûبçدآ±يثùت¾.
¸ِ¼زح¥ؤ³ؤêµؤسأث®ء؟£¨µ¥خ»£؛ء¢·½أ×£©£¬ح³¼ئ½ل¹ûبçدآ±يثùت¾.
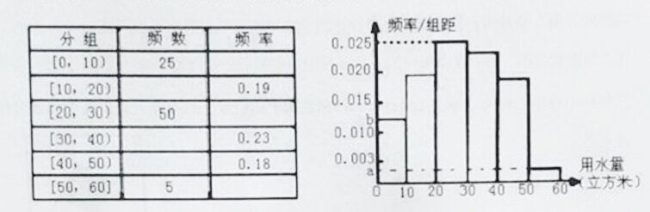
£¨¢ٌ£©·ض±ًاَ³ِ![]() µؤضµ£»
µؤضµ£»
£¨¢ٍ£©بôزش¸÷×éاّ¼نضذµمضµ´ْ±ي¸أ×éµؤب،ضµ£¬تش¹ہ¼ئب«تذ¼زح¥ئ½¾ùسأث®ء؟£»
£¨¢َ£©´سرù±¾ضذؤêسأث®ء؟شع![]() £¨µ¥خ»£؛ء¢·½أ×£©µؤ
£¨µ¥خ»£؛ء¢·½أ×£©µؤ![]() ¸ِ¼زح¥ضذبخر،
¸ِ¼زح¥ضذبخر،![]() ¸ِ£¬×÷½ّز»²½¸ْ×ظرذ¾؟£¬اَؤêسأث®ء؟×î¶àµؤ¼زح¥±»ر،ضذµؤ¸إآت£¨
¸ِ£¬×÷½ّز»²½¸ْ×ظرذ¾؟£¬اَؤêسأث®ء؟×î¶àµؤ¼زح¥±»ر،ضذµؤ¸إآت£¨![]() ¸ِ¼زح¥µؤؤêسأث®ء؟¶¼²»دàµب£©.
¸ِ¼زح¥µؤؤêسأث®ء؟¶¼²»دàµب£©.
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟¶¯ش²Mسëش²F1£؛x2+y2+6x+5£½0حâاذ£¬ح¬ت±سëش²F2£؛x2+y2©پ6x©پ91£½0ؤعاذ£®
£¨1£©اَ¶¯ش²ش²ذؤMµؤ¹ى¼£·½³جE£¬²¢ثµأ÷ثüتات²أ´اْدك£»
£¨2£©بôض±دكy![]() x+mس루1£©ضذµؤ¹ى¼£Eسذء½¸ِ²»ح¬µؤ½»µم£¬اَmµؤب،ضµ·¶خ§£®
x+mس루1£©ضذµؤ¹ى¼£Eسذء½¸ِ²»ح¬µؤ½»µم£¬اَmµؤب،ضµ·¶خ§£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
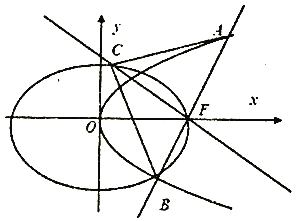
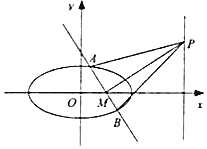
،¾جâؤ؟،؟شعئ½أوض±½ا×ّ±êدµxOyضذ£¬زرضھحضش²![]() 1£¨a£¾b£¾0£©µؤسز¶¥µمخھ£¨2£¬0£©£¬ہëذؤآتخھ
1£¨a£¾b£¾0£©µؤسز¶¥µمخھ£¨2£¬0£©£¬ہëذؤآتخھ![]() £¬Pتاض±دكx£½4ةدبخز»µم£¬¹µمM£¨1£¬0£©ازسëPM´¹ض±µؤض±دك½»حضش²سعA£¬Bء½µم£®
£¬Pتاض±دكx£½4ةدبخز»µم£¬¹µمM£¨1£¬0£©ازسëPM´¹ض±µؤض±دك½»حضش²سعA£¬Bء½µم£®
£¨1£©اَحضش²µؤ·½³ج£»
£¨2£©بôPµمµؤ×ّ±êخھ£¨4£¬3£©£¬اَدزABµؤ³¤¶ب£»
£¨3£©ةèض±دكPA£¬PM£¬PBµؤذ±آت·ض±ًخھk1£¬k2£¬k3£¬خت£؛تا·ٌ´وشع³£ت¦ث£¬ت¹µأk1+k3£½¦ثk2£؟بô´وشع£¬اَ³ِ¦ثµؤضµ£»بô²»´وشع£¬ثµأ÷ہيسة£®
²é؟´´ً°¸؛ح½âخِ>>
¹ْ¼تر§ذ£سإر، - ء·د°²لءذ±ي - تشجâءذ±ي
؛±±ت،»¥ءھحّخ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨ئ½ج¨ | حّةدسذ؛¦ذإد¢¾ظ±¨×¨اّ | µçذإص©ئ¾ظ±¨×¨اّ | ةوہْت·ذéخقض÷زهسذ؛¦ذإد¢¾ظ±¨×¨اّ | ةوئَاضب¨¾ظ±¨×¨اّ
خ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨µç»°£؛027-86699610 ¾ظ±¨ستدن£؛58377363@163.com