
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程,并说明它为何种曲线;
的直角坐标方程,并说明它为何种曲线;
(Ⅱ)设点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:高中数学 来源: 题型:
【题目】已知在正三棱柱![]() 中,侧棱长
中,侧棱长![]() 为3,H、G分别是AB,
为3,H、G分别是AB,![]() 中点.
中点.
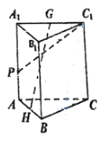
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,求此三棱柱的侧面积;
,求此三棱柱的侧面积;
(3)若P为侧棱![]() 上一点,且
上一点,且![]() ,
,![]() 与平面
与平面![]() 所成角大小为
所成角大小为![]() ,求此三棱柱的体积.
,求此三棱柱的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年我国全面建成小康社会,其中小康生活的住房标准是城镇人均住房建筑面积30平方米. 下表为2007年—2016年中,我区城镇和农村人均住房建筑面积统计数据. 单位:平方米.
2007年 | 2008年 | 2009年 | 2010年 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 | |
城镇 | 18.66 | 20.25 | 22.79 | 25 | 27.1 | 28.3 | 31.6 | 32.9 | 34.6 | 36.6 |
农村 | 23.3 | 24.8 | 26.5 | 27.9 | 30.7 | 32.4 | 34.1 | 37.1 | 41.4 | 45.8 |
(1)现从上述表格中随机抽取一年数据,试估计该年城镇人均住房建筑面积达到小康生活住房标准的概率;
(2)现从上述表格中随机抽取连续两年数据,求这两年中城镇人均住房建筑面积增长不少于2平方米的概率;
(3)将城镇和农村的人均住房建筑面积经四舍五入取整后作为样本数据.记2012—2016年中城镇人均住房面积的方差为![]() ,农村人均住房面积的方差为
,农村人均住房面积的方差为![]() ,判断
,判断![]() 与
与![]() 的大小.(只需写出结论).
的大小.(只需写出结论).
(注:方差![]() ,其中
,其中![]() 为
为 ![]()
![]() ,……
,…… ![]() 的平均数)
的平均数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某兴趣小组在科学馆的帕斯卡三角仪器前进行探究实验.如图所示,每次使一个实心小球从帕斯卡三角仪器的顶部入口落下,当它在依次碰到每层的菱形挡板时,会等可能地向左或者向右落下,在最底层的7个出口处各放置一个容器接住小球,该小组连续进行200次试验,并统计容器中的小球个数得到柱状图:
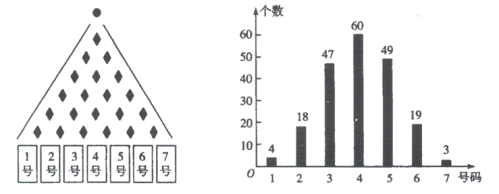
(Ⅰ)用该实验来估测小球落入4号容器的概率,若估测结果的误差小于![]() ,则称该实验是成功的.试问:该兴趣小组进行的实验是否成功?(误差
,则称该实验是成功的.试问:该兴趣小组进行的实验是否成功?(误差![]() )
)
(Ⅱ)再取3个小球进行试验,设其中落入4号容器的小球个数为![]() ,求
,求![]() 的分布列与数学期望.(计算时采用概率的理论值)
的分布列与数学期望.(计算时采用概率的理论值)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 是椭圆
是椭圆![]() 的一个顶点,
的一个顶点,![]() 的短轴是圆
的短轴是圆![]() 的直径,直线
的直径,直线![]() ,
,![]() 过点P且互相垂直,
过点P且互相垂直,![]() 交椭圆
交椭圆![]() 于另一点D,
于另一点D,![]() 交圆
交圆![]() 于A,B两点
于A,B两点
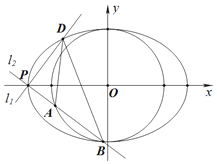
![]() Ⅰ
Ⅰ![]() 求椭圆
求椭圆![]() 的标准方程;
的标准方程;
![]() Ⅱ
Ⅱ![]() 求
求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】央视传媒为了解央视举办的“朗读者”节目的收视时间情况,随机抽取了某市名![]() 观众进行调查,其中有
观众进行调查,其中有![]() 名男观众和
名男观众和![]() 名女观众,将这
名女观众,将这![]() 名观众收视时间编成如图所示的茎叶图(单位:分钟),收视时间在
名观众收视时间编成如图所示的茎叶图(单位:分钟),收视时间在![]() 分钟以上(包括
分钟以上(包括![]() 分钟)的称为“朗读爱好者”,收视时间在
分钟)的称为“朗读爱好者”,收视时间在![]() 分钟以下(不包括
分钟以下(不包括![]() 分钟)的称为“非朗读爱好者”.
分钟)的称为“非朗读爱好者”.

(1)若采用分层抽样的方法从“朗读爱好者”和“非朗读爱好者”中随机抽取![]() 名,再从这
名,再从这![]() 名观众中任选
名观众中任选![]() 名,求至少选到
名,求至少选到![]() 名“朗读爱好者”的概率;
名“朗读爱好者”的概率;
(2)若从收视时间在40分钟以上(包括40分钟)的所有观众中选出男、女观众各1名,求选出的这两名观众时间相差5分钟以上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某老师是省级课题组的成员,主要研究课堂教学目标达成度,为方便研究,从实验班中随机抽取30次的随堂测试成绩进行数据分析![]() 已知学生甲的30次随堂测试成绩如下
已知学生甲的30次随堂测试成绩如下![]() 满分为100分
满分为100分![]() :
:

![]() 把学生甲的成绩按
把学生甲的成绩按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6组,列出频率分布表,并画出频率分布直方图;
分成6组,列出频率分布表,并画出频率分布直方图;
![]() 规定随堂测试成绩80分以上
规定随堂测试成绩80分以上![]() 含80分
含80分![]() 为优秀,为帮助学生甲提高成绩,选取学生乙,对甲与乙的随堂测试成绩进行对比分析,甲与乙测试成绩是否为优秀相互独立
为优秀,为帮助学生甲提高成绩,选取学生乙,对甲与乙的随堂测试成绩进行对比分析,甲与乙测试成绩是否为优秀相互独立![]() 已知甲成绩优秀的概率为
已知甲成绩优秀的概率为![]() 以频率估计概率
以频率估计概率![]() ,乙成绩优秀的概率为
,乙成绩优秀的概率为![]() ,若
,若![]() ,则此二人适合为学习上互帮互助的“对子”
,则此二人适合为学习上互帮互助的“对子”![]() 在一次随堂测试中,记
在一次随堂测试中,记![]() 为两人中获得优秀的人数,已知
为两人中获得优秀的人数,已知![]() ,问二人是否适合结为“对子”?
,问二人是否适合结为“对子”?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com