
【题目】已知函数![]() 在
在![]() 处取得极值.
处取得极值.
![]() Ⅰ
Ⅰ![]() 求实数a的值;
求实数a的值;
![]() Ⅱ
Ⅱ![]() 若关于x的方程
若关于x的方程![]() 在
在![]() 上恰有两个不相等的实数根,求实数b的取值范围;
上恰有两个不相等的实数根,求实数b的取值范围;
![]() Ⅲ
Ⅲ![]() 证明:
证明:![]() 参考数据:
参考数据:![]() .
.
【答案】(1)0;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)求导,由f′(1)=0构造方程求出a;(2)由(1)将方程f(x)+2x=x2+b化简,令g(x)=x2-3x+lnx+b(x>0),求导,研究当x变化时,g′(x),g(x)的变化情况,确定函数的最值,从而建立不等式组,即可求得结论;(3)设φ(x)=lnx-![]() (x2-1),求导,根据函数的单调性得当x≥2时,
(x2-1),求导,根据函数的单调性得当x≥2时,![]() >2
>2![]() ,从而累加可得结论.
,从而累加可得结论.
(1)f′(x)=1-![]() ,∵x=1是f(x)的一个极值点,∴f′(1)=0,即1-
,∵x=1是f(x)的一个极值点,∴f′(1)=0,即1-![]() =0,∴a=0.
=0,∴a=0.
经检验满足题意.
(2)由(1)得f(x)=x-lnx,∴f(x)+2x=x2+b即x-lnx+2x=x2+b,∴x2-3x+lnx+b=0,
设g(x)=x2-3x+lnx+b(x>0),
则g′(x)=2x-3+![]() =
=![]()
=![]() .
.
由g′(x)>0得0<x<![]() 或x>1,由g′(x)<0得
或x>1,由g′(x)<0得![]() <x<1,
<x<1,
∴当x∈![]() ,(1,+∞)时,函数g(x)单调递增,x∈
,(1,+∞)时,函数g(x)单调递增,x∈![]() 时,函数g(x)单调递减,
时,函数g(x)单调递减,
当x=1时,g(x)极小值=g(1)=b-2,g![]() =b-
=b-![]() -ln2,g(2)=b-2+ln2,
-ln2,g(2)=b-2+ln2,
∵方程f(x)+2x=x2+b在![]() 上恰有两个不相等的实数根,
上恰有两个不相等的实数根,
∴ 即
即 解得
解得![]() +ln2≤b<2.
+ln2≤b<2.
(3)证明:∵k-f(k)=lnk,∴![]()
![]() >
>![]() .
.
![]() +
+![]() +
+![]() +…+
+…+![]() >
>![]() (n∈N,n≥2)
(n∈N,n≥2)
设φ(x)=lnx-![]() (x2-1),则φ′(x)=
(x2-1),则φ′(x)=![]() -
-![]() =
=![]() =-
=-![]()
当x≥2时,φ′(x)<0,∴函数y=φ(x)在[2,+∞)上是减函数,
∴φ(x)≤φ(2)=ln2-![]() <0,∴lnx<
<0,∴lnx<![]() (x2-1).
(x2-1).
∴当x≥2时,![]() >
>![]() =
=![]()
=2![]() ,
,
∴![]() +
+![]() +
+![]() +…+
+…+![]() >2
>2![]()
=2![]() =
=![]() .
.
∴原不等式成立.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:
【题目】(选做题)
A.[选修4-2:矩阵与变换](本小题满分10分)
已知m,n∈R,向量![]() 是矩阵
是矩阵![]() 的属于特征值3的一个特征向量,求矩阵M及另一个特征值.
的属于特征值3的一个特征向量,求矩阵M及另一个特征值.
B.[选修4-4:坐标系与参数方程](本小题满分10分)
在平面直角坐标系xOy中,已知直线![]() 的参数方程为
的参数方程为![]() ( t为参数),椭圆C的参数方程为
( t为参数),椭圆C的参数方程为![]() .设直线
.设直线![]() 与椭圆C交于A,B两点,求线段AB的长.
与椭圆C交于A,B两点,求线段AB的长.
C.[选修4-5:不等式选讲](本小题满分10分)
已知x,y,z均是正实数,且![]() 求证:
求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程,并说明它为何种曲线;
的直角坐标方程,并说明它为何种曲线;
(Ⅱ)设点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为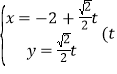 为参数
为参数![]() ,直线
,直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点.
两点.
(1)若点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值;
的值;
(2)求曲线![]() 的内接矩形周长的最大值.
的内接矩形周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是空气质量的一个重要指标,我国
是空气质量的一个重要指标,我国![]() 标准采用世卫组织设定的最宽限值,即
标准采用世卫组织设定的最宽限值,即![]() 日均值在
日均值在![]() 以下空气质量为一级,在
以下空气质量为一级,在![]() 之间空气质量为二级,在
之间空气质量为二级,在![]() 以上空气质量为超标.如图是某地
以上空气质量为超标.如图是某地![]() 月
月![]() 日到
日到![]() 日
日![]() 日均值(单位:
日均值(单位:![]() )的统计数据,则下列叙述不正确的是( )
)的统计数据,则下列叙述不正确的是( )
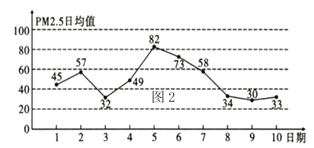
A.从![]() 日到
日到![]() 日,
日,![]() 日均值逐渐降低
日均值逐渐降低
B.这![]() 天的
天的![]() 日均值的中位数是
日均值的中位数是![]()
C.这![]() 天中
天中![]() 日均值的平均数是
日均值的平均数是![]()
D.从这![]() 天的日均
天的日均![]() 监测数据中随机抽出一天的数据,空气质量为一级的概率是
监测数据中随机抽出一天的数据,空气质量为一级的概率是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱锥D-ABC中,二面角A-BC-D的大小为90°,且∠BDC=90°,∠ABC=30°,BC=3,![]() .
.
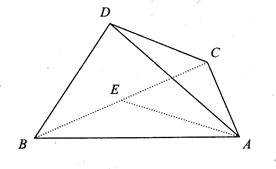
(1)求证:AC⊥平面BCD;
(2)二面角B-AC-D为45°,且E为线段BC的中点,求直线AE与平面ACD所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图甲所示, ![]() 是梯形
是梯形![]() 的高,
的高, ![]() ,
, ![]() ,
, ![]() ,现将梯形
,现将梯形![]() 沿
沿![]() 折起如图乙所示的四棱锥
折起如图乙所示的四棱锥![]() ,使得
,使得![]() ,点
,点![]() 是线段
是线段![]() 上一动点.
上一动点.
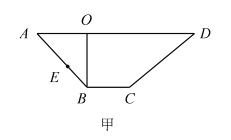
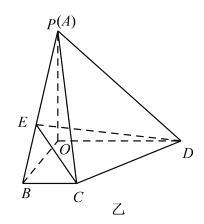
(1)证明: ![]() 和
和![]() 不可能垂直;
不可能垂直;
(2)当![]() 时,求
时,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设椭圆![]() :
: ![]() ,长轴的右端点与抛物线
,长轴的右端点与抛物线![]() :
: ![]() 的焦点
的焦点![]() 重合,且椭圆
重合,且椭圆![]() 的离心率是
的离心率是![]() .
.
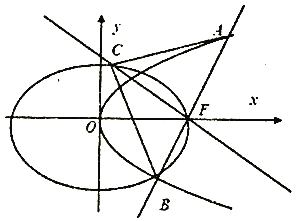
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过![]() 作直线
作直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
, ![]() 两点,过
两点,过![]() 且与直线
且与直线![]() 垂直的直线交椭圆
垂直的直线交椭圆![]() 于另一点
于另一点![]() ,求
,求![]() 面积的最小值,以及取到最小值时直线
面积的最小值,以及取到最小值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动圆M与圆F1:x2+y2+6x+5=0外切,同时与圆F2:x2+y2﹣6x﹣91=0内切.
(1)求动圆圆心M的轨迹方程E,并说明它是什么曲线;
(2)若直线y![]() x+m与(1)中的轨迹E有两个不同的交点,求m的取值范围.
x+m与(1)中的轨迹E有两个不同的交点,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com