
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的图象在点(1,
的图象在点(1, ![]() )处的切线方程;
)处的切线方程;
(Ⅱ)讨论函数![]() 的单调区间;
的单调区间;
(Ⅲ)已知![]() ,对于函数
,对于函数![]() 图象上任意不同的两点
图象上任意不同的两点![]() ,其中
,其中![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,记
,记![]() ,若
,若![]() 求证
求证![]()
【答案】(Ⅰ) ![]() ;(Ⅱ)答案见解析;(Ⅲ)证明见解析.
;(Ⅱ)答案见解析;(Ⅲ)证明见解析.
【解析】【试题分析】(Ⅰ)由题设条件先求出函数![]() 导数,再借助导数的几何意义求出切线的斜率
导数,再借助导数的几何意义求出切线的斜率![]() ;(Ⅱ)先求函数
;(Ⅱ)先求函数![]() 的导数
的导数![]() 再依据实数
再依据实数![]() 的取值范围进行分类求出其单调区间;(Ⅲ)分别求出k=
的取值范围进行分类求出其单调区间;(Ⅲ)分别求出k=![]()
![]() 和
和![]() 将问题转化为证明
将问题转化为证明![]() ,然后设
,然后设![]() 再构造函数
再构造函数![]() ,最后借助导数知识推断函数
,最后借助导数知识推断函数![]() 在
在![]() 内单调递减,进而推得
内单调递减,进而推得![]() 从而证得
从而证得![]() :
:
解析:(Ⅰ)当![]() 时,
时, ![]()
![]()
![]()
又![]()
![]() 函数
函数![]() 的图象在点(1,
的图象在点(1, ![]() )处的切线方程为:
)处的切线方程为: ![]() ,
,
即![]()
(Ⅱ) ![]() 的定义域为
的定义域为![]()
![]()
当![]() 时,
时, ![]() 在
在![]() 上恒成立,
上恒成立, ![]() 在定义域内单调递增;
在定义域内单调递增;
当![]() 时,令
时,令![]() 解得,
解得, ![]()
![]()
则 时,
时, ![]() ,
, ![]() 单调递增;
单调递增;
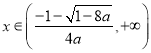 时,
时, ![]() ,
, ![]() 单调递减;
单调递减;
综上, ![]() 时,
时, ![]() 的单调递增区间为
的单调递增区间为![]() ;
;
![]() 时,
时, ![]() 的单调递增区间为
的单调递增区间为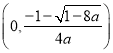 ,
,
![]() 的单调递增区间为
的单调递增区间为
(Ⅲ)证明: ![]()
![]()
![]()
![]() ,
,
又![]() ,
, ![]()
![]()
![]()
要证: ![]() ,只需证
,只需证![]()
即证: ![]() ,设
,设![]()
令![]() 则
则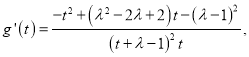
令![]()
对称轴![]() .
.
![]()
![]() ,故
,故![]() 在
在![]() 内单调递减,则
内单调递减,则![]() ;
;
故![]() .
.


科目:高中数学 来源: 题型:
【题目】中国传统文化中很多内容体现了数学的对称美,如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分展现了相互转化、对称统一的形式美、和谐美,给出定义:能够将圆![]() 的周长和面积同时平分的函数称为这个圆的“优美函数”,给出下列命题:
的周长和面积同时平分的函数称为这个圆的“优美函数”,给出下列命题:

①对于任意一个圆![]() ,其“优美函数“有无数个”;
,其“优美函数“有无数个”;
②函数![]() 可以是某个圆的“优美函数”;
可以是某个圆的“优美函数”;
③正弦函数![]() 可以同时是无数个圆的“优美函数”;
可以同时是无数个圆的“优美函数”;
④函数![]() 是“优美函数”的充要条件为函数
是“优美函数”的充要条件为函数![]() 的图象是中心对称图形.
的图象是中心对称图形.
其中正确的命题是:( )
A. ①③ B. ①③④ C. ②③ D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举行了以“重温时代经典,唱响回声嘹亮”为主题的“红歌”歌咏比赛. 该校高一年级有1,2,3,4四个班参加了比赛,其中有两个班获奖. 比赛结果揭晓之前,甲同学说:“两个获奖班级在2班、3班、4班中”,乙同学说:“2班没有获奖,3班获奖了”,丙同学说:“1班、4班中有且只有一个班获奖”,丁同学说:“乙说得对”. 已知这四人中有且只有两人的说法是正确的,则这两人是
A. 乙,丁 B. 甲,丙 C. 甲,丁 D. 乙,丙
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为函数
为函数![]() 图象上一点,
图象上一点, ![]() 为坐标原点,记直线
为坐标原点,记直线![]() 的斜率
的斜率![]() .
.
(1)若函数![]() 在区间
在区间![]() 上存在极值,求实数
上存在极值,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)求证: ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当前,网购已成为现代大学生的时尚。某大学学生宿舍4人参加网购,约定:每个人通过掷一枚质地均匀的骰子决定自己去哪家购物,掷出点数为5或6的人去淘宝网购物,掷出点数小于5的人去京东商城购物,且参加者必须从淘宝网和京东商城选择一家购物.
(1)求这4个人中恰有1人去淘宝网购物的概率;
(2)用![]() 分别表示这4个人中去淘宝网和京东商城购物的人数,记
分别表示这4个人中去淘宝网和京东商城购物的人数,记![]() ,求随机变量
,求随机变量![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 为曲线
为曲线![]() 上任意一点,且
上任意一点,且![]() 到定点
到定点![]() 的距离比到
的距离比到![]() 轴的距离多1.
轴的距离多1.
(1)求曲线![]() 的方程;
的方程;
(2)点![]() 为曲线
为曲线![]() 上一点,过点
上一点,过点![]() 分别作倾斜角互补的直线
分别作倾斜角互补的直线![]() ,
, ![]() 与曲线
与曲线![]() 分别交于
分别交于![]() ,
, ![]() 两点,过点
两点,过点![]() 且与
且与![]() 垂直的直线
垂直的直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,若
两点,若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①频率是反映事件发生的频繁程度,概率反映事件发生的可能性大小;
②做n次随机试验,事件A发生m次,则事件A发生的频率![]() 就是事件A的概率;
就是事件A的概率;
③百分率是频率,但不是概率;
④频率是不能脱离n次试验的试验值,而概率是具有确定性的不依赖于试验次数的理论值;
⑤频率是概率的近似值,概率是频率的稳定值.
其中正确的是____(填序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com