
【题目】在平面直角坐标系中,点![]() 为曲线
为曲线![]() 上任意一点,且
上任意一点,且![]() 到定点
到定点![]() 的距离比到
的距离比到![]() 轴的距离多1.
轴的距离多1.
(1)求曲线![]() 的方程;
的方程;
(2)点![]() 为曲线
为曲线![]() 上一点,过点
上一点,过点![]() 分别作倾斜角互补的直线
分别作倾斜角互补的直线![]() ,
, ![]() 与曲线
与曲线![]() 分别交于
分别交于![]() ,
, ![]() 两点,过点
两点,过点![]() 且与
且与![]() 垂直的直线
垂直的直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,若
两点,若![]() ,求点
,求点![]() 的坐标.
的坐标.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】第35届牡丹花会期间,我班有5名学生参加志愿者服务,服务场所是王城公园和牡丹公园.
(1)若学生甲和乙必须在同一个公园,且甲和丙不能在同一个公园,则共有多少种不同的分配方案?
(2)每名学生都被随机分配到其中的一个公园,设![]() 分别表示5名学生分配到王城公园和牡丹公园的人数,记
分别表示5名学生分配到王城公园和牡丹公园的人数,记![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的图象在点(1,
的图象在点(1, ![]() )处的切线方程;
)处的切线方程;
(Ⅱ)讨论函数![]() 的单调区间;
的单调区间;
(Ⅲ)已知![]() ,对于函数
,对于函数![]() 图象上任意不同的两点
图象上任意不同的两点![]() ,其中
,其中![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,记
,记![]() ,若
,若![]() 求证
求证![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
性别 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)请根据上面的数据分析该地区的老年人需要志愿者提供帮助与性别有关吗
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学开展了一系列的读书教育活动,为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查,下图是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,若将日均课外阅读时间不低于60分钟的学生称为“读书迷”,低于60分钟的学生称为“非读书迷”.
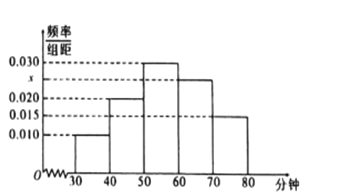
(Ⅰ) 求![]() 的值并估计全校3000名学生中“读书迷”大概有多少?(将频率视为概率)
的值并估计全校3000名学生中“读书迷”大概有多少?(将频率视为概率)
(Ⅱ)根据已知条件完成下面![]() 的列联表,并据此判断是否有99%的把握认为“读书迷”与性别有关?
的列联表,并据此判断是否有99%的把握认为“读书迷”与性别有关?
非读书迷 | 读书迷 | 合计 | |
男 | 15 | ||
女 | 45 | ||
合计 |
附: 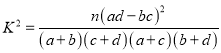 ,
, ![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人组成一个小组参加电视台举办的听曲猜歌名活动,在每一轮活动中,依次播放三首乐曲,然后甲猜第一首,乙猜第二首,丙猜第三首,若有一人猜错,则活动立即结束;若三人均猜对,则该小组进入下一轮,该小组最多参加三轮活动.已知每一轮甲猜对歌名的概率是![]() ,乙猜对歌名的概率是
,乙猜对歌名的概率是![]() ,丙猜对歌名的概率是
,丙猜对歌名的概率是![]() ,甲、乙、丙猜对与否互不影响.
,甲、乙、丙猜对与否互不影响.
(I)求该小组未能进入第二轮的概率;
(Ⅱ)记乙猜歌曲的次数为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com