Question

【题目】某中学开展了一系列的读书教育活动，为了解本校学生课外阅读情况，学校随机抽取了100名学生对其课外阅读时间进行调查，下图是根据调查结果绘制的学生日均课外阅读时间（单位：分钟）的频率分布直方图，若将日均课外阅读时间不低于60分钟的学生称为“读书迷”，低于60分钟的学生称为“非读书迷”．

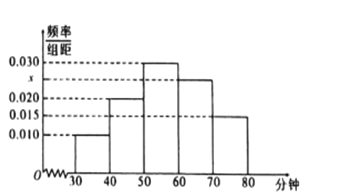
(Ⅰ) 求的值并估计全校3000名学生中“读书迷”大概有多少？（将频率视为概率）

(Ⅱ)根据已知条件完成下面的列联表，并据此判断是否有99%的把握认为“读书迷”与性别有关？

	非读书迷	读书迷	合计
男		15
女			45
合计

附： ， ．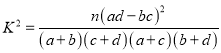

	0．100	0．050	0．025	0．010	0．001
	2．706	3．841	5．024	6．635	10．828

Answer 1

【答案】（Ⅰ）人;（Ⅱ）见解析．

【解析】【试题分析】（1）依据题设中的频率分布直方图求解；（2）借助题设条件及2×2列联表中的数据计算、分析和推断进行求解：

（Ⅰ）由已知得，得．

因为，

所以全校3000名学生中“读书迷”大概有人．

（Ⅱ）列联表如下：

	非读书迷	读书迷	合计
男	40	15	55
女	20	25	45
合计	60	40	100

．

∵，∴有99%的把握认为“读书迷”与性别有关．