
| A. | (-∞,1] | B. | [1,2017) | C. | (-∞,1) | D. | (1,2017) |
分析 画出f(x)的图象,可得1-2a=2b-1=-log2017(c-1)=log2017(d-1)=t,(0<t<1),分别用t表示a,b,c,d,再由指数和对数的运算性质及不等式的性质,即可得到所求范围.
解答 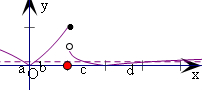 解:函数f(x)=$\left\{\begin{array}{l}|{2^x}-1|,x≤1\\|{log_{2017}}(x-1)|,x>1\end{array}$,
解:函数f(x)=$\left\{\begin{array}{l}|{2^x}-1|,x≤1\\|{log_{2017}}(x-1)|,x>1\end{array}$,
若方程f(x)=t有四个不同的实数根a,b,c,d,且a<b<c<d,
可得1-2a=2b-1=-log2017(c-1)=log2017(d-1)=t,(0<t<1),
即有2a=1-t,2b=1+t,
a+b=log2(1-t)+log2(1+t)=log2(1-t2)<0,
c-1=2017-t,d-1=2017t,
$\frac{1}{c}+\frac{1}{d}$=$\frac{1}{1+201{7}^{-t}}$+$\frac{1}{1+201{7}^{t}}$=$\frac{201{7}^{t}+1}{1+201{7}^{t}}$=1,
则a+b+$\frac{1}{c}+\frac{1}{d}$<1.
故选:C.
点评 本题考查方程根的情况,考查数形结合思想方法和转化思想,同时考查对数和指数的运算性质,不等式的性质,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{4}$ | B. | $\frac{7}{5}$ | C. | $\frac{8}{5}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
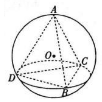 体积为$18\sqrt{3}$的正三棱锥A-BCD的每个顶点都在半径为R的球O的球面上,球心O在此三棱锥内部,且R:BC=2:3,点E为线段BD上一点,且DE=2EB,过点E作球O的截面,则所得截面圆面积的取值范围是( )
体积为$18\sqrt{3}$的正三棱锥A-BCD的每个顶点都在半径为R的球O的球面上,球心O在此三棱锥内部,且R:BC=2:3,点E为线段BD上一点,且DE=2EB,过点E作球O的截面,则所得截面圆面积的取值范围是( )| A. | [4π,12π] | B. | [8π,16π] | C. | [8π,12π] | D. | [12π,16π] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 时间 | 11日 | 12日 | 13日 | 14日 | 15日 | 16日 | 17日 | 18日 | 19日 | 20日 |
| AQI | 149 | 143 | 251 | 254 | 138 | 55 | 69 | 102 | 243 | 269 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要 | B. | 必要不充分 | ||
| C. | 充分不必要 | D. | 既不充分也不必要 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{53}{4}$ | B. | 10 | C. | $\frac{36}{5}$ | D. | 17 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com