
Ζ÷Έω Μ·ΦρfΘ®xΘ©=sinΠΊxΘ§ΗυΨί’ΐœ“Κ· ΐΒΡΒΞΒς–‘ΒΟ≥ωfΘ®xΘ©ΒΡΒΞΒς‘ω«χΦδΘ§¥”ΕχΝ–≥ω≤ΜΒ» ΫΫβ≥ωΠΊΒΡΖΕΈßΘ°
Ϋβ¥π ΫβΘΚfΘ®xΘ©=$\overrightarrow{a}•\overrightarrow{b}$+1=2sin$\frac{ΠΊ}{2}$xcos$\frac{ΠΊ}{2}$x=sinΠΊxΘ§
Νν-$\frac{Π–}{2}$+2kΠ–ΓήΠΊxΓή$\frac{Π–}{2}$+2kΠ–Θ§ΫβΒΟ-$\frac{Π–}{2ΠΊ}$+$\frac{2kΠ–}{ΠΊ}$ΓήxΓή$\frac{Π–}{2ΠΊ}$+$\frac{2kΠ–}{ΠΊ}$Θ§kΓ ZΘ§
ΓΏΠΊΘΨ0Θ§
ΓύfΘ®xΘ©ΒΡ“ΜΗωΒΞΒς‘ω«χΦδΈΣ[-$\frac{Π–}{2ΠΊ}$Θ§$\frac{Π–}{2ΠΊ}$]Θ§
Γύ$\left\{\begin{array}{l}{\frac{Π–}{4}Γή\frac{Π–}{2ΠΊ}}\\{-\frac{Π–}{5}Γί-\frac{Π–}{2ΠΊ}}\end{array}\right.$Θ§ΫβΒΟ0ΘΦΠΊΓή2Θ°
Ι ¥πΑΗΈΣΘ®0Θ§2]Θ°
ΒψΤά ±ΨΧβΩΦ≤ιΝΥ»ΐΫ«Κ· ΐΒΡΚψΒ»±δΜΜΘ§’ΐœ“Κ· ΐΒΡΆΦœσ”κ–‘÷ Θ§ τ”Ύ÷–ΒΒΧβΘ°


 »ΐ–¬Ωλ≥ΒΫπ≈Τ÷ή÷ήΝΖœΒΝ–¥πΑΗ
»ΐ–¬Ωλ≥ΒΫπ≈Τ÷ή÷ήΝΖœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | Θ®-ΓόΘ§1] | BΘ° | [1Θ§2017Θ© | CΘ° | Θ®-ΓόΘ§1Θ© | DΘ° | Θ®1Θ§2017Θ© |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | ΟϋΧβpΓ≈qΈΣΦΌΟϋΧβ | BΘ° | ΟϋΧβpΓΡqΈΣ’φΟϋΧβ | ||
| CΘ° | ΟϋΧβpΓΡΘ®©VqΘ©ΈΣ’φΟϋΧβ | DΘ° | ΟϋΧβpΓ≈Θ®©VqΘ©ΈΣΦΌΟϋΧβ | ||
| EΘ° | ΟϋΧβpΓ≈qΈΣΦΌΟϋΧβ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
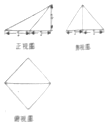
| AΘ° | 3Π– | BΘ° | 5Π– | CΘ° | 10Π– | DΘ° | 20Π– |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | y=Γάx | BΘ° | $y=Γά\sqrt{2}x$ | CΘ° | $y=Γά\sqrt{3}x$ | DΘ° | y=Γά2x |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | $\sqrt{2}$ | BΘ° | $2\sqrt{2}$ | CΘ° | $\sqrt{3}$ | DΘ° | $2\sqrt{3}$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com