
分析 (1)先求出M,再利用绝对值不等式证明即可;
(2)利用作差方法,比较|4ab-1|与2|b-a|的大小.
解答 (1)证明:记f(x)=|x+2|-|1-x|=$\left\{\begin{array}{l}{-3,x≤-2}\\{2x+1,-2<x<1}\\{3,x≥1}\end{array}\right.$,
∴由0<2x+1<2,解得-$\frac{1}{2}$<x<$\frac{1}{2}$,∴M=(-$\frac{1}{2}$,$\frac{1}{2}$)
∴|a+$\frac{1}{2}$b|≤|a|+$\frac{1}{2}$|b|$<\frac{1}{2}+\frac{1}{2}×\frac{1}{2}$=<$\frac{3}{4}$;
(2)解:由(1)可得a2<$\frac{1}{4}$,b2<$\frac{1}{4}$,
∴(4ab-1)2-4(b-a)2=(4a2-1)(4b2-1)>0,
∴|4ab-1|>2|b-a|.
点评 本题考查绝对值不等式的运用,考查作差方法的运用,考查学生的计算能力,属于中档题.


 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:选择题
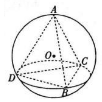 体积为$18\sqrt{3}$的正三棱锥A-BCD的每个顶点都在半径为R的球O的球面上,球心O在此三棱锥内部,且R:BC=2:3,点E为线段BD上一点,且DE=2EB,过点E作球O的截面,则所得截面圆面积的取值范围是( )
体积为$18\sqrt{3}$的正三棱锥A-BCD的每个顶点都在半径为R的球O的球面上,球心O在此三棱锥内部,且R:BC=2:3,点E为线段BD上一点,且DE=2EB,过点E作球O的截面,则所得截面圆面积的取值范围是( )| A. | [4π,12π] | B. | [8π,16π] | C. | [8π,12π] | D. | [12π,16π] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{53}{4}$ | B. | 10 | C. | $\frac{36}{5}$ | D. | 17 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com