
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 的直线
的直线![]() 交
交![]() 于
于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() 到
到![]() 轴的距离比
轴的距离比![]() 小
小![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)若![]() ,求
,求![]() 的方程.
的方程.
【答案】:(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)由抛物线的定义,可知![]() 等于点
等于点![]() 到
到![]() 的准线的距离,即
的准线的距离,即![]() ,又因为点
,又因为点![]() 到
到![]() 轴的距离比
轴的距离比![]() 小
小![]() ,所以
,所以![]() ,解出
,解出![]() 的方程为
的方程为![]()
(Ⅱ)由题意可设![]() 的方程为
的方程为![]() ),联立方程组由韦达定理,得
),联立方程组由韦达定理,得![]() 又
又![]() ,所以
,所以![]() ,所以
,所以![]() ,从而
,从而![]() ,即
,即![]() ,即可解出
,即可解出![]() ,写出直线方程.
,写出直线方程.
试题解析:(Ⅰ) ![]() 的准线方程为
的准线方程为![]() ,
,
由抛物线的定义,可知![]() 等于点
等于点![]() 到
到![]() 的准线的距离,即
的准线的距离,即![]() ,
,
又因为点![]() 到
到![]() 轴的距离比
轴的距离比![]() 小
小![]() ,
,
所以![]() ,
,
故![]() ,解得
,解得![]() ,
,
所以![]() 的方程为
的方程为![]()
(Ⅱ)由(Ⅰ)得![]() 的焦点
的焦点![]() ,因为直线
,因为直线![]() 交
交![]() 于
于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,所以
,所以![]() 的斜率存在且不为
的斜率存在且不为![]() ,故可设
,故可设![]() 的方程为
的方程为![]() ,
,
则![]() .
.
联立方程组![]() ,消去
,消去![]() ,得
,得![]()
![]() ,
,
由韦达定理,得![]()
设点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,则
,则![]()
又![]() ,所以
,所以![]() .
.
又![]() 在同一直线上,所以
在同一直线上,所以![]() ,从而
,从而![]() ,即
,即![]() ,
,
因为![]() ,
,
所以![]() ,整理,得
,整理,得![]() ,
,
故![]() ,解得
,解得![]() ,
,
所以![]() 的方程为
的方程为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】函数 ![]() 是定义在(﹣1,1)上的奇函数,且
是定义在(﹣1,1)上的奇函数,且 ![]() .
.
(1)确定函数的解析式;
(2)证明函数f(x)在(﹣1,1)上是增函数;
(3)解不等式f(t﹣1)+f(t)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣x3+ax2+1,(a∈R).
(1)若f(x)图象上横坐标为1的点处存在垂直于y轴的切线,求a的值;
(2)若f(x)在区间(﹣1,2)内有两个不同的极值点,求a取值范围;
(3)当a=1时,是否存在实数m,使得函数g(x)=x4﹣5x3+(2﹣m)x2+1的图象于函数f(x)的图象恰有三个不同的交点,若存在,试求出实数m的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F(0,1),直线l:y=﹣1,P为平面上的动点,过点P作直线l的垂线,垂足为Q,且 ![]() .
.
(1)求动点P的轨迹C的方程;
(2)已知圆M过定点D(0,2),圆心M在轨迹C上运动,且圆M与x轴交于A、B两点,设|DA|=l1 , |DB|=l2 , 求 ![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】五一节期间,某商场为吸引顾客消费推出一项优惠活动,活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券.(假定指针等可能地停在任一位置,指针落在区域的边界时,重新转一次)指针所在的区域及对应的返劵金额见表.
例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.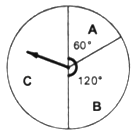
(1)已知顾客甲消费后获得n次转动转盘的机会,已知他每转一次转盘指针落在区域边界的概率为p,每次转动转盘的结果相互独立,设ξ为顾客甲转动转盘指针落在区域边界的次数,ξ的数学期望Eξ= ![]() ,方差Dξ=
,方差Dξ= ![]() ,求n、p的值;
,求n、p的值;
(2)顾客乙消费280元,并按规则参与了活动,他获得返券的金额记为η(元).求随机变量η的分布列和数学期望.
指针位置 | A区域 | B区域 | C区域 |
返券金额(单位:元) | 60 | 30 | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com