
����Ŀ����һ���ڼ䣬ij�̳�Ϊ�����˿������Ƴ�һ���Żݻ����������£����Ѷ�ÿ��100Ԫ��ת����ͼ��ʾ��ת��һ�Σ��������Ӧ���ķ�ȯ�����ٶ�ָ��ȿ��ܵ�ͣ����һλ�ã�ָ����������ı߽�ʱ������תһ�Σ�ָ�����ڵ�����Ӧ�ķ�����������
���磺����218Ԫ����ת��ת��2�Σ�����õķ�ȯ��������ν��֮�ͣ�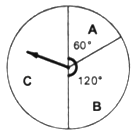
��1����֪�˿ͼ����Ѻ���n��ת��ת�̵Ļ��ᣬ��֪��ÿתһ��ת��ָ����������߽�ĸ���Ϊp��ÿ��ת��ת�̵Ľ������������Ϊ�˿ͼ�ת��ת��ָ����������߽�Ĵ������ε���ѧ����E��= ![]() ������D��=
������D��= ![]() ����n��p��ֵ��
����n��p��ֵ��
��2���˿�������280Ԫ��������������˻������÷�ȯ�Ľ���Ϊ�ǣ�Ԫ��������������ǵķֲ��к���ѧ������
ָ��λ�� | A���� | B���� | C���� |
��ȯ����λ��Ԫ�� | 60 | 30 | 0 |
���𰸡�
��1���⣺������֪���η��Ӷ���ֲ��Ρ�B��n��p����
�� ![]() ��
��
�� ![]() ��
��
������ã� ![]() ��
��
��2���⣺��ָ������A��B��C����ֱ��Ϊ�¼�A��B��C��
�� ![]() ��
��
������ã��ù˿Ϳ�ת��ת��2�Σ�
��������ǵĿ���ֵΪ0��30��60��90��120��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
����������ǵķֲ���Ϊ��
P | 0 | 30 | 60 | 90 | 120 |
�� |
|
|
|
|
|
����ѧ���� ![]()
����������1��������֪���η��Ӷ���ֲ��Ρ�B��n��p�����ɴ����ö���ֲ������������n��p��ֵ����2����ָ������A��B��C����ֱ��Ϊ�¼�A��B��C���� ![]() ��������ã��ù˿Ϳ�ת��ת��2�Σ���������ǵĿ���ֵΪ0��30��60��90��120���ֱ������Ӧ�ĸ��ʣ��ɴ��������������ǵķֲ��к���ѧ������
��������ã��ù˿Ϳ�ת��ת��2�Σ���������ǵĿ���ֵΪ0��30��60��90��120���ֱ������Ӧ�ĸ��ʣ��ɴ��������������ǵķֲ��к���ѧ������
�����㾫����������Ĺؼ�����������ɢ�������������ֲ��е����֪ʶ���������������Ʒ����������У������������X����ȡ��ֵ�����ǿ���һ������һһ�г����������������������ɢ�������������ɢ����������ķֲ��У�һ���,����ɢ���������X����ȡ��ֵΪx1,x2,.....,xi,......,xn��Xȡÿһ��ֵ xi(i=1,2,......���ĸ���P(��=xi����Pi����Ʊ�Ϊ��ɢ���������X �ĸ��ʷֲ�����Ʒֲ��У�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Բ![]() ����Ϊ
����Ϊ![]() ������Բ
������Բ![]() ��ֱ��
��ֱ��![]() ���У�
����
��1������Բ![]() �ı����̣�
�ı����̣�
��2������![]() �Ķ�ֱ������Բ
�Ķ�ֱ������Բ![]() ����
����![]() ���㣬��
���㣬��![]() Ϊ����ԭ�㣬�Ƿ���ڳ���
Ϊ����ԭ�㣬�Ƿ���ڳ���![]() ��ʹ��
��ʹ��![]() ����˵������.
����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼΪij��2017��2��28����տ�������ָ������ͼ.
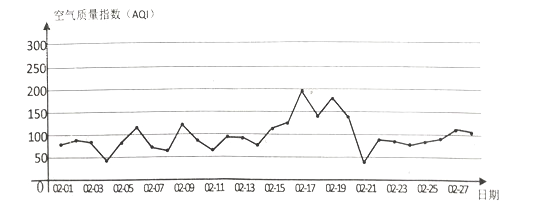
���й�����������������ƽ̨�ṩ�Ŀ�������ָ�������£�

��1�����������������ͼ��ȫ�·���Ƶ�ʷֲ�ֱ��ͼ������Ǧ��Ϳ�ھ����������������2�·ݿ�������ָ��������ݵ�ƽ����������С�����һλ����
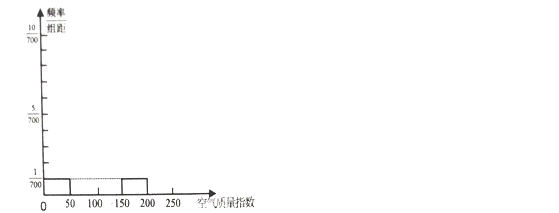
��2���о���Ա���֣���������ָ��������![]() ��ȼ���ŷŵ�
��ȼ���ŷŵ�![]() ������Ŀ����������ع�ϵ����
������Ŀ����������ع�ϵ����![]() Ϊ��λ���±�����
Ϊ��λ���±�����![]() ��
��![]() ��������ݣ�
��������ݣ�

��![]() ����
����![]() �Ļع鷽�̣������Ƶ�
�Ļع鷽�̣������Ƶ�![]() �ŷ�����
�ŷ�����![]() ʱ��
ʱ�� ![]() ��ֵ.
��ֵ.
������С���˷���ع鷽�̵�ϵ����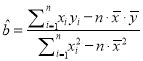 ��
�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�溯��f��x������f��x+2��=f��x��2������x�ʣ�0��1��ʱ��f��x��=3x �� ��f�� ![]() ��= ��
��= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����f��x��=|x+1|+|x��1|��
��1����f��x����x+2�Ľ⼯��
��2��������ʽf��x����log2��a2��4a+12��������ʵ��a���������x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() ��,������
��,������![]() �Ľ���Ϊ
�Ľ���Ϊ![]() ,����
,����![]() ��ֱ��
��ֱ��![]() ��
��![]() ��
��![]() ����,��
����,��![]() ���ڵ�
���ڵ�![]() ��
��![]() ��ľ����
��ľ����![]() С
С![]() .
.
(��)��![]() �ķ��̣�
�ķ��̣�
������![]() ����
����![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x�����溯����g��x����ż���������ڹ���������{x|x��R��x�١�1}������f��x��+g��x��= ![]() ��
��
��1����f��x����g��x���Ľ���ʽ��
��2����h��x��=f��x����g��x������h�� ![]() ����
����
��3����ֵ��h��2��+h��3��+h��4��+��+h��2016��+h�� ![]() ��+h��
��+h�� ![]() ��+h��
��+h�� ![]() ��+��+h��
��+��+h�� ![]() ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �У�
�У� ![]() ƽ��
ƽ��![]() ����
����![]() ����
����![]() ��
��![]() �ϣ���
�ϣ���![]() .
.

������֤�� ![]() ƽ��
ƽ��![]() ��
��
����������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��������
��������![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ����
����![]() ��
��![]() ͼ���ϣ���
ͼ���ϣ���![]() ����СֵΪ
����СֵΪ![]() .
.
��1��������![]() ��ͨ�ʽ��
��ͨ�ʽ��
��2������![]() ����
����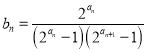 ��������
��������![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ����֤��
����֤�� ![]() .
.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com