
【题目】已知函数f(x)是奇函数,g(x)是偶函数,且在公共定义域{x|x∈R且x≠±1}上满足f(x)+g(x)= ![]() .
.
(1)求f(x)和g(x)的解析式;
(2)设h(x)=f(x)﹣g(x),求h( ![]() );
);
(3)求值:h(2)+h(3)+h(4)+…+h(2016)+h( ![]() )+h(
)+h( ![]() )+h(
)+h( ![]() )+…+h(
)+…+h( ![]() ).
).
【答案】
(1)解:由题意,f(x)+g(x)= ![]() ,①
,①
f(﹣x)+g(﹣x)= ![]() ,即﹣f(x)+g(x)=﹣
,即﹣f(x)+g(x)=﹣ ![]() ,②
,②
由①②联立解得f(x)= ![]() ,g(x)=
,g(x)= ![]()
(2)解:h(x)=f(x)﹣g(x)═ ![]() =
= ![]() ,
,
∴h( ![]() )=
)= ![]() =
= ![]()
(3)解:∵h(x)+h( ![]() )=
)= ![]() =1,
=1,
∴h(2)+h(3)+h(4)+…+h(2016)+h( ![]() )+h(
)+h( ![]() )+h(
)+h( ![]() )+…+h(
)+…+h( ![]() )
)
=[h(2)+h( ![]() )]+[h(3)+h(
)]+[h(3)+h( ![]() )]+…+h(2016)+h(
)]+…+h(2016)+h( ![]() )]
)]
=2015
【解析】(1)由f(x)+g(x)= ![]() ,得﹣f(x)+g(x)=﹣
,得﹣f(x)+g(x)=﹣ ![]() ,联立方程组能求出f(x),g(x).(2)由h(x)=f(x)﹣g(x)═
,联立方程组能求出f(x),g(x).(2)由h(x)=f(x)﹣g(x)═ ![]() =
= ![]() ,能求出h(
,能求出h( ![]() ).(3)由h(x)+h(
).(3)由h(x)+h( ![]() )=
)= ![]() =1,能求出h(2)+h(3)+h(4)+…+h(2016)+h(
=1,能求出h(2)+h(3)+h(4)+…+h(2016)+h( ![]() )+h(
)+h( ![]() )+h(
)+h( ![]() )+…+h(
)+…+h( ![]() )的值.
)的值.
【考点精析】利用函数奇偶性的性质和函数的值对题目进行判断即可得到答案,需要熟知在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇;函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法.


科目:高中数学 来源: 题型:
【题目】甲乙两家快递公司其“快递小哥”的日工资方案如下:甲公司规定底薪![]() 元,每单抽成
元,每单抽成![]() 元;乙公司规定底薪
元;乙公司规定底薪![]() 元,每日前
元,每日前![]() 单无抽成,超过
单无抽成,超过![]() 单的部分每单抽成
单的部分每单抽成![]() 元
元
(1)设甲乙快递公司的“快递小哥”一日工资![]() (单位:元)与送货单数
(单位:元)与送货单数![]() 的函数关系式为
的函数关系式为![]() ,求
,求![]() ;
;
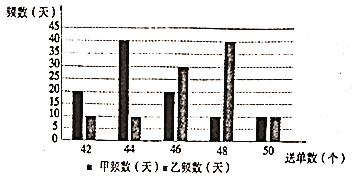
(2)假设同一公司的“快递小哥”一日送货单数相同,现从两家公司各随机抽取一名“快递小哥”,并记录其![]() 天的送货单数,得到如下条形图:
天的送货单数,得到如下条形图:
若将频率视为概率,回答下列问题:
①记乙快递公司的“快递小哥”日工资为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
②小赵拟到两家公司中的一家应聘“快递小哥”的工作,如果仅从日收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】五一节期间,某商场为吸引顾客消费推出一项优惠活动,活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券.(假定指针等可能地停在任一位置,指针落在区域的边界时,重新转一次)指针所在的区域及对应的返劵金额见表.
例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.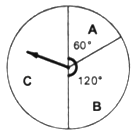
(1)已知顾客甲消费后获得n次转动转盘的机会,已知他每转一次转盘指针落在区域边界的概率为p,每次转动转盘的结果相互独立,设ξ为顾客甲转动转盘指针落在区域边界的次数,ξ的数学期望Eξ= ![]() ,方差Dξ=
,方差Dξ= ![]() ,求n、p的值;
,求n、p的值;
(2)顾客乙消费280元,并按规则参与了活动,他获得返券的金额记为η(元).求随机变量η的分布列和数学期望.
指针位置 | A区域 | B区域 | C区域 |
返券金额(单位:元) | 60 | 30 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有能力互异的3人应聘同一公司,他们按照报名顺序依次接受面试,经理决定“不录用第一个接受面试的人,如果第二个接受面试的人比第一个能力强,就录用第二个人,否则就录用第三个人”,记该公司录用到能力最强的人的概率为p,录用到能力中等的人的概率为q,则(p,q)=( )
A.( ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() )
)
C.( ![]() ,
, ![]() )
)
D.( ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2﹣a2x+3.
(1)若a=2,求f(x)在[﹣1,2]上的最值;
(2)若f(x)在(﹣ ![]() ,1)上是减函数,求a的取值范围.
,1)上是减函数,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与圆
与圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(1)求圆![]() 的直角坐标方程及弦
的直角坐标方程及弦![]() 的长;
的长;
(2)动点![]() 在圆
在圆![]() 上(不与
上(不与![]() ,
, ![]() 重合),试求
重合),试求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 在平面直角坐标系
在平面直角坐标系![]() 下的参数方程为
下的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(1)求曲线![]() 的普通方程及极坐标方程;
的普通方程及极坐标方程;
(2)直线![]() 的极坐标方程是
的极坐标方程是![]() ,射线
,射线![]() :
: ![]() 与曲线
与曲线![]() 交于点
交于点![]() 与直线
与直线![]() 交于点
交于点![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com