
【题目】如图,已知椭圆![]()
![]() (
(![]() )与圆
)与圆![]() :
:![]() 在第一象限相交于点
在第一象限相交于点![]() ,椭圆
,椭圆![]() 的左、右焦点
的左、右焦点![]() ,
,![]() 都在圆
都在圆![]() 上,且线段
上,且线段![]() 为圆
为圆![]() 的直径.
的直径.

(1)求椭圆![]() 的方程;
的方程;
(2)设过点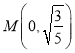 的动直线
的动直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 为坐标原点,证明:
为坐标原点,证明:![]() 为定值,并求出这个定值.
为定值,并求出这个定值.
【答案】(1)![]() ;(2)证明见解析,定值为
;(2)证明见解析,定值为![]() .
.
【解析】
(1)由圆的方程可得与![]() 轴的交点坐标即椭圆的焦点坐标,和圆的半径,由题意可得
轴的交点坐标即椭圆的焦点坐标,和圆的半径,由题意可得![]() 的值,再由存在求出
的值,再由存在求出![]() ,再由椭圆的定义可得椭圆的方程;
,再由椭圆的定义可得椭圆的方程;
(2)分直线的斜率存在和不存在两种情况讨论,设直线的方程与椭圆联立求出两根之和及两根之积,进而求出数量积![]() 的值为定值.
的值为定值.
解:(1)在圆![]() 的方程中,令
的方程中,令![]() ,得
,得![]() ,即
,即![]() ,所以
,所以![]() .
.
将圆![]() 的方程化为
的方程化为![]() ,则圆
,则圆![]() 半径为
半径为![]() ,所以
,所以![]() .
.
连结![]() ,因为点
,因为点![]() 在圆
在圆![]() 上,
上,![]() 为圆
为圆![]() 的直径,则
的直径,则![]() .
.
又![]() ,则
,则![]() .
.
据椭圆定义,![]() ,则
,则![]() .
.
从而![]() ,所以椭圆
,所以椭圆![]() 的方程是
的方程是![]() ;
;
(2)当直线![]() 的斜率存在时,设
的斜率存在时,设![]() 的斜率为
的斜率为![]() ,则
,则![]() 的方程为
的方程为![]() ,代入椭圆方程,得
,代入椭圆方程,得
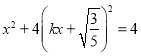 ,即
,即![]() .
.
设点![]() ,
,![]() .则
.则![]() ,
,![]() .
.
所以![]()
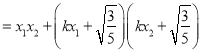
![]()
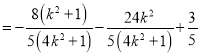
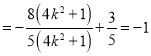 ,
,
当![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 与
与![]() 轴重合,此时点
轴重合,此时点![]() ,
,![]() ,
,![]() ,
,
综上分析,![]() 为定值.
为定值.


科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() ,
,![]() 点是它的右端点,弦
点是它的右端点,弦![]() 过椭圆的中心
过椭圆的中心![]() ,
,![]() ,
,![]() .
.

(1)求椭圆的标准方程;
(2)设![]() 、
、![]() 为圆上不重合的两点,
为圆上不重合的两点,![]() 的平分线总是垂直于
的平分线总是垂直于![]() 轴,且存在实数
轴,且存在实数![]() ,使得
,使得![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为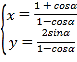 (
(![]() 为参数).以
为参数).以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ),将曲线
),将曲线![]() 向左平移2个单位长度得到曲线
向左平移2个单位长度得到曲线![]() .
.
(1)求曲线![]() 的普通方程和极坐标方程;
的普通方程和极坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某销售公司在当地![]() 、
、![]() 两家超市各有一个销售点,每日从同一家食品厂一次性购进一种食品,每件200元,统一零售价每件300元,两家超市之间调配食品不计费用,若进货不足食品厂以每件250元补货,若销售有剩余食品厂以每件150回收.现需决策每日购进食品数量,为此搜集并整理了
两家超市各有一个销售点,每日从同一家食品厂一次性购进一种食品,每件200元,统一零售价每件300元,两家超市之间调配食品不计费用,若进货不足食品厂以每件250元补货,若销售有剩余食品厂以每件150回收.现需决策每日购进食品数量,为此搜集并整理了![]() 、
、![]() 两家超市往年同期各50天的该食品销售记录,得到如下数据:
两家超市往年同期各50天的该食品销售记录,得到如下数据:
销售件数 | 8 | 9 | 10 | 11 |
频数 | 20 | 40 | 20 | 20 |
以这些数据的频数代替两家超市的食品销售件数的概率,记![]() 表示这两家超市每日共销售食品件数,
表示这两家超市每日共销售食品件数,![]() 表示销售公司每日共需购进食品的件数.
表示销售公司每日共需购进食品的件数.
(1)求![]() 的分布列;
的分布列;
(2)以销售食品利润的期望为决策依据,在![]() 与
与![]() 之中选其一,应选哪个?
之中选其一,应选哪个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂加工的零件按箱出厂,每箱有10个零件,在出厂之前需要对每箱的零件作检验,人工检验方法如下:先从每箱的零件中随机抽取4个零件,若抽取的零件都是正品或都是次品,则停止检验;若抽取的零件至少有1个至多有3个次品,则对剩下的6个零件逐一检验.已知每个零件检验合格的概率为0.8,每个零件是否检验合格相互独立,且每个零件的人工检验费为2元.
(1)设1箱零件人工检验总费用为![]() 元,求
元,求![]() 的分布列;
的分布列;
(2)除了人工检验方法外还有机器检验方法,机器检验需要对每箱的每个零件作检验,每个零件的检验费为1.6元.现有1000箱零件需要检验,以检验总费用的数学期望为依据,在人工检验与机器检验中,应该选择哪一个?说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有一个“引葭赴岸”问题:“今有池方一丈,葭生其中央.出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何?”其意思为“今有水池1丈见方(即![]() 尺),芦苇生长在水的中央,长出水面的部分为1尺.将芦苇向池岸牵引,恰巧与水岸齐接(如图所示).试问水深、芦苇的长度各是多少?假设
尺),芦苇生长在水的中央,长出水面的部分为1尺.将芦苇向池岸牵引,恰巧与水岸齐接(如图所示).试问水深、芦苇的长度各是多少?假设![]() ,现有下述四个结论:
,现有下述四个结论:
①水深为12尺;②芦苇长为15尺;③![]() ;④
;④![]() .
.
其中所有正确结论的编号是( )
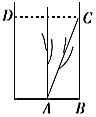
A.①③B.①③④C.①④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的偶函数
上的偶函数![]() 满足
满足![]() ,且
,且![]() ,当
,当![]() 时,
时,![]() .已知方程
.已知方程![]() 在区间
在区间![]() 上所有的实数根之和为
上所有的实数根之和为![]() .将函数
.将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,则
的图象,则![]() __________,
__________,![]() __________.
__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com