
分析 求出向量的长度和数量积,结合向量夹角公式进行求解即可.
解答 解:∵$\overrightarrow{a}$=(1,$\sqrt{3}$),$\overrightarrow{b}$=(-2,2$\sqrt{3}$),
∴|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=$\sqrt{(-2)^{2}+(2\sqrt{3})^{2}}$=4,
$\overrightarrow{a}$•$\overrightarrow{b}$=-2+2$\sqrt{3}$×$\sqrt{3}$=6-2=4,
则cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{4}{2×4}=\frac{1}{2}$,
则<$\overrightarrow{a}$,$\overrightarrow{b}$>=60°,
故答案为:60°
点评 本题主要考查向量数量积的应用,根据向量夹角公式是解决本题的关键.比较基础.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | A+B与C是互斥事件,也是对立事件 | |
| B. | B+C与D是互斥事件,也是对立事件 | |
| C. | A+C与B+D是互斥事件,但不是对立事件 | |
| D. | A与B+C+D是互斥事件,也是对立事件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,0)∪(9,+∞) | C. | (9,+∞) | D. | (-∞,1)∪(9,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
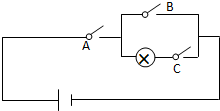 如图所示电路,有A、B、C三个开关,每个开关开或关的概率都是$\frac{1}{2}$,且相互独立,则灯泡亮的概率( )
如图所示电路,有A、B、C三个开关,每个开关开或关的概率都是$\frac{1}{2}$,且相互独立,则灯泡亮的概率( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{16}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com