
分析 ①根据指数函数的性质进行判断,
②根据对数的运算法则进行判断
③根据函数的运算性质进行运算,
④根据偶函数的定义进行判断,
⑤根据集合关系,利用排除法进行判断.
解答 解:①当x=1时,f(1)=a0+2=1+2=3,则函数的图象经过定点(1,3);故①正确,
②已知x=log23,4y=$\frac{8}{3}$,则22y=$\frac{8}{3}$,2y=log2$\frac{8}{3}$,则x+2y=log23+log2$\frac{8}{3}$=log2($\frac{8}{3}$×3)=log28=3;故②正确,
③若f(x)=x3+ax-6,且f(-2)=6,则-23-2a-6=6,即a=-10,
则f(2)=23-2×10-6=-18,故③错误;
④函数的定义域为{x|x≠0},关于原点对称,f(x)=x($\frac{1}{1-{2}^{x}}$-$\frac{1}{2}$)=x•$\frac{1+{2}^{x}}{2(1-{2}^{x})}$,
则f(-x)=-x•$\frac{1+{2}^{-x}}{2(1-{2}^{-x})}$=-x•$\frac{{2}^{x}+1}{2({2}^{x}-1)}$=x•$\frac{1+{2}^{x}}{2(1-{2}^{x})}$=f(x),
即有f(x)为偶函数.则f(x)=x($\frac{1}{1-2^x}$-$\frac{1}{2}$)为偶函数;故④正确,
⑤已知集合A={-1,1},B={x|mx=1},且B⊆A,当m=0时,B=∅,也满足条件.,故⑤错误,
故正确的是①②④,
故答案为:①②④
点评 本题主要考查命题的真假判断,涉及指数函数的性质,函数奇偶性的判断,以及对数的运算法则,综合性较强,涉及的知识点较多.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:选择题
| A. | ?x∈(0,+∞),x2≠x-1 | B. | ?x∈(0,+∞),x2=x-1 | ||
| C. | ?x0∉(0,+∞),x${\;}_{0}^{2}$≠x0-1 | D. | ?x0∈(0,+∞),x${\;}_{0}^{2}$≠x0-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
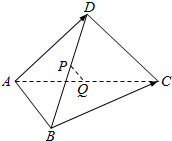 如图,P,Q分别为四边形ABCD的对角线BD,AC的中点,$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,向量$\overrightarrow{a}$,$\overrightarrow{b}$不共线,试用$\overrightarrow{a}$,$\overrightarrow{b}$表示向量$\overrightarrow{PQ}$.
如图,P,Q分别为四边形ABCD的对角线BD,AC的中点,$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,向量$\overrightarrow{a}$,$\overrightarrow{b}$不共线,试用$\overrightarrow{a}$,$\overrightarrow{b}$表示向量$\overrightarrow{PQ}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com