
分析 由已知设a=2k,b=3k,c=4k,k>0,利用余弦定理能求出cosC,由此能求出tanC.
解答 解:∵△ABC边BC,CA,AB上的高分别为ha、hb、hc,且ha:hb:hc=6:4:3,
$S△ABC=\frac{1}{2}a{h}_{a}=\frac{1}{2}b{h}_{b}=\frac{1}{2}c{h}_{c}$,
∴$a:b:c=\frac{1}{{h}_{a}}:\frac{1}{{h}_{b}}:\frac{1}{{h}_{c}}$=$\frac{1}{6}:\frac{1}{4}:\frac{1}{3}$=2:3:4,
设a=2k,b=3k,c=4k,k>0,
则cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{4{k}^{2}+9{k}^{2}-16{k}^{2}}{2×2k×3k}$=-$\frac{1}{4}$,
∴sinC=$\sqrt{1-\frac{1}{16}}$=$\frac{\sqrt{15}}{4}$,
tanC=$\frac{sinC}{cosC}$=$\frac{\frac{\sqrt{15}}{4}}{-\frac{1}{4}}$=-$\sqrt{15}$.
故答案为:-$\sqrt{15}$.
点评 本题考查正切函数的求法,是中档题,解题时要认真审题,注意余弦定理的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 410-1 | B. | $\frac{{4}^{10}-1}{3}$ | C. | 210-1 | D. | $\frac{{2}^{10}-1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | [-1,+∞) | C. | (-∞,+∞) | D. | (-∞,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
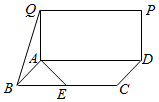 如图,四边形ABCD和ADPQ均为长方形,它们所在的平面互相垂直,且AB=AQ=$\frac{1}{2}$AD,E为BC的中点,则异面直线BQ与AE所成的角大小为60°.
如图,四边形ABCD和ADPQ均为长方形,它们所在的平面互相垂直,且AB=AQ=$\frac{1}{2}$AD,E为BC的中点,则异面直线BQ与AE所成的角大小为60°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -8 | B. | -$\frac{1}{8}$ | C. | 8 | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
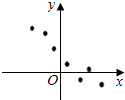
| A. | $\widehat{y}$=1.5x+2 | B. | $\widehat{y}$=-1.5x+2 | C. | $\widehat{y}$=1.5x-2 | D. | $\widehat{y}$=-1.5x-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com