
 如图,正四面体ABCD的顶点C在平面α内,且直线BC与平面α所成角为15°,顶点B在平面α上的射影为点O,当顶点A与点O的距离最大时,直线CD与平面α所成角的正弦值为$\frac{\sqrt{6}}{6}$.
如图,正四面体ABCD的顶点C在平面α内,且直线BC与平面α所成角为15°,顶点B在平面α上的射影为点O,当顶点A与点O的距离最大时,直线CD与平面α所成角的正弦值为$\frac{\sqrt{6}}{6}$. 分析 当A,B,O,C四点共面时,|OA|最大,过D作平面ABOC的垂线DN,则垂足为△ABC的中心,求出N到平面α的距离d,则直线CD与平面α所成角的正弦值为$\frac{d}{CD}$.
解答 解: 当四边形ABOC为平面四边形时,点A到点O的距离最大.
当四边形ABOC为平面四边形时,点A到点O的距离最大.
此时平面ABOC⊥平面α,过D作DN⊥平面ABOC,垂足为N,
则N为正三角形ABC的中心.
设正四面体的边长为1,则CN=$\frac{2}{3}$CP=$\frac{\sqrt{3}}{3}$,
∵∠BCO=15°,∠BCP=30°,∴∠OCN=45°,
∴N到平面α的距离d=$\frac{\sqrt{3}}{3}×\frac{\sqrt{2}}{2}$=$\frac{\sqrt{6}}{6}$.
过D作DM⊥平面α,垂足为M,则DM=d=$\frac{\sqrt{6}}{6}$,
∴直线CD与平面α所成角的正弦值为$\frac{DM}{CD}$=$\frac{\sqrt{6}}{6}$.
故答案为:$\frac{{\sqrt{6}}}{6}$
点评 本题考查了线面角的计算,常见几何体的结构特征,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2.00 | 2.20 | 2.60 | 3.20 | 3.40 | 4.00 |
| y | 0.22 | 0.20 | 0.30 | 0.48 | 0.56 | 0.60 |
| $\sum_{i=1}^{6}({y}_{i}-\overline{y})^{2}$ | y=a+bx | y=c+dlgx |
| $\sum_{i=1}^{6}({y}_{i}-\stackrel{∧}{{y}_{i}})^{2}$ | $\sum_{i=1}^{6}({y}_{i}-\stackrel{∧}{{y}_{i}})^{2}$ | |
| 0.15 | 0.13 | 0.01 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{1}{2}$-$\frac{\sqrt{3}}{4}$ | D. | $\frac{1}{2}$+$\frac{{\sqrt{3}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
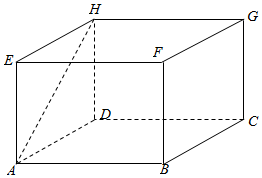 如图所示,长方体ABCD-EFGH,底面是边长为2$\sqrt{3}$的正方形,DH=2,P为AH中点.
如图所示,长方体ABCD-EFGH,底面是边长为2$\sqrt{3}$的正方形,DH=2,P为AH中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com