
分析 设等比数列的公比为q,由等差数列的中项的性质和等比数列的通项公式,化简整理即可得到所求值.
解答 解:设各项都是正数,且公比为q的等比数列{an}中,
3a1,$\frac{1}{2}$a3,2a2成等差数列,
可得a3=3a1+2a2,
即为a1q2=3a1+2a1q,
即q2-2q-3=0,解得q=3或q=-1(舍去),
则an=a13n-1,
则$\frac{{a}_{10}+{a}_{12}+{a}_{15}+{a}_{19}+{a}_{20}+{a}_{23}}{{a}_{8}+{a}_{10}+{a}_{13}+{a}_{17}+{a}_{18}+{a}_{21}}$=$\frac{{a}_{10}(1+{q}^{2}+{q}^{5}+{q}^{9}+{q}^{10}+{q}^{13})}{{a}_{8}(1+{q}^{2}+{q}^{5}+{q}^{9}+{q}^{10}+{q}^{13})}$
=$\frac{{a}_{10}}{{a}_{8}}$=q2=9.
故答案为:9.
点评 本题考查等比数列的通项公式的运用,同时考查等差数列中项的性质,考查化简整理的运算能力,属于基础题.


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
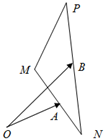 如图,已知$\overrightarrow{OA}$=$\overrightarrow a$,$\overrightarrow{OB}$=$\overrightarrow b$,且|$\overrightarrow b$|=2|$\overrightarrow a$|=2,任意点M关于点A的对称点为N,点N关于点B的对称点为P,则$\overrightarrow{MP}$•($\overrightarrow{OA}$+$\overrightarrow{OB}$)=( )
如图,已知$\overrightarrow{OA}$=$\overrightarrow a$,$\overrightarrow{OB}$=$\overrightarrow b$,且|$\overrightarrow b$|=2|$\overrightarrow a$|=2,任意点M关于点A的对称点为N,点N关于点B的对称点为P,则$\overrightarrow{MP}$•($\overrightarrow{OA}$+$\overrightarrow{OB}$)=( )| A. | 6 | B. | -6 | C. | 3 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2+1>2a | B. | |x+$\frac{1}{x}$|≥2 | C. | $\frac{a+b}{\sqrt{ab}}$≤2 | D. | |sinx+$\frac{4}{sinx}$|≥4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com