
【题目】已知f(x)为二次函数,且![]() .
.
(1)求f(x)的表达式;
(2)判断函数![]() 在(0,+∞)上的单调性,并证明.
在(0,+∞)上的单调性,并证明.
【答案】(1)![]() ;(2)增函数,证明见解析.
;(2)增函数,证明见解析.
【解析】
(1)利用题中所给的条件,先设出函数的解析式,利用![]() ,将式子化为恒等式,利用对应项系数相等,得到方程组,求得结果;
,将式子化为恒等式,利用对应项系数相等,得到方程组,求得结果;
(2)先化简函数解析式,利用单调性的定义,证明得到函数的单调性,得到结果.
(1)设f(x)=ax2+bx+c(a≠0),
由条件得:a(x+1)2+b(x+1)+c+a(x﹣1)2+b(x﹣1)+c=2x2﹣4x,
从而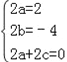 , 解得:
, 解得: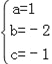 ,
,
所以f(x)=x2﹣2x﹣1;
(2)函数g(x)=![]() 在(0,+∞)上单调递增.
在(0,+∞)上单调递增.
理由如下:g(x)=![]() =
=![]() ,
,
设设任意x1,x2∈(0,+∞),且x1<x2,
则g(x1)﹣g(x2)=![]() ﹣(
﹣(![]() )=(x1﹣x2)(1+
)=(x1﹣x2)(1+![]() ),
),
∵x1,x2∈(0,+∞),且x1<x2,
∴x1﹣x2<0,1+![]() >0,
>0,
∴g(x1)﹣g(x2)<0,即g(x1)<g(x2),
所以函数g(x)=![]() 在(0,+∞)上单调递增.
在(0,+∞)上单调递增.


科目:高中数学 来源: 题型:
【题目】某地某路无人驾驶公交车发车时间间隔![]() (单位:分钟)满足
(单位:分钟)满足![]() ,
,![]() .经测算,该路无人驾驶公交车载客量
.经测算,该路无人驾驶公交车载客量![]() 与发车时间间隔
与发车时间间隔![]() 满足:
满足: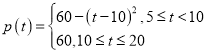 ,其中
,其中![]() .
.
(1)求![]() ,并说明
,并说明![]() 的实际意义;
的实际意义;
(2)若该路公交车每分钟的净收益![]() (元),问当发车时间间隔为多少时,该路公交车每分钟的净收益最大?并求每分钟的最大净收益.
(元),问当发车时间间隔为多少时,该路公交车每分钟的净收益最大?并求每分钟的最大净收益.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代儒家要求学生掌握六种基本才艺:礼、乐、射、御、书、数,简称“六艺”,某高中学校为弘扬“六艺”的传统文化,分别进行了主题为“礼、乐、射、御、书、数”六场传统文化知识竞赛,现有甲、乙、丙三位选手进入了前三名的最后角逐,规定:每场知识竞赛前三名的得分都分别为![]()
![]() 且
且![]() ;选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为
;选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为![]() 分,乙和丙最后得分都是
分,乙和丙最后得分都是![]() 分,且乙在其中一场比赛中获得第一名,下列说法正确的是( )
分,且乙在其中一场比赛中获得第一名,下列说法正确的是( )
A. 乙有四场比赛获得第三名
B. 每场比赛第一名得分![]() 为
为![]()
C. 甲可能有一场比赛获得第二名
D. 丙可能有一场比赛获得第一名
查看答案和解析>>
科目:高中数学 来源: 题型:
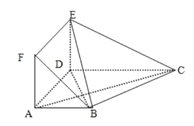
【题目】在多面体![]() 中,底面
中,底面![]() 是梯形,四边形
是梯形,四边形![]() 是正方形,
是正方形,![]() ,
,![]() ,面
,面![]() 面
面![]() ,
,![]() .
.![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)设![]() 为线段
为线段![]() 上一点,
上一点,![]() ,试问在线段
,试问在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,试指出点
,若存在,试指出点![]() 的位置;若不存在,说明理由?
的位置;若不存在,说明理由?
(3)在(2)的条件下,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了鼓励节约用电,辽宁省实行阶梯电价制度,其中每户的用电单价与户年用电量的关系如下表所示.
分档 | 户年用电量(度) | 用电单价(元/度) |
第一阶梯 |
| 0.5 |
第二阶梯 |
| 0.55 |
第三阶梯 |
| 0.80 |
记用户年用电量为![]() 度时应缴纳的电费为
度时应缴纳的电费为![]() 元.
元.
(1)写出![]() 的解析式;
的解析式;
(2)假设居住在沈阳的范伟一家2018年共用电3000度,则范伟一家2018年应缴纳电费多少元?
(3)居住在大连的张莉一家在2018年共缴纳电费1942元,则张莉一家在2018年用了多少度电?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年1月31日晚上月全食的过程分为初亏、食既、食甚、生光、复圆五个阶段,月食的初亏发生在19时48分,20时51分食既,食甚时刻为21时31分,22时08分生光,直至23时12分复圆.全食伴随有蓝月亮和红月亮,全食阶段的“红月亮”将在食甚时刻开始,生光时刻结東,一市民准备在19:55至21:56之间的某个时刻欣赏月全食,则他等待“红月亮”的时间不超过30分钟的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com