
| A. | (-2,2) | B. | (-∞,-2)∪(0,2) | C. | (-∞,-2)∪(2,+∞) | D. | (-2,0]∪(2,+∞) |
分析 根据函数的奇偶性、单调性画出函数f(x)的示意图,将不等式等价转化,由图象求出不等式解集.
解答 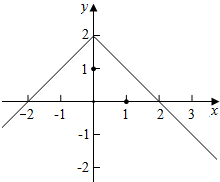 解:∵偶函数f(x)在(-∞,0]上为增函数,又f(-2)=0,
解:∵偶函数f(x)在(-∞,0]上为增函数,又f(-2)=0,
∴函数f(x)在(0,+∞)上为减函数,且f(-2)=f(2)=0,
画出函数f(x)的示意图如图所示:
∵不等式xf(x)>0等价为$\left\{\begin{array}{l}{x>0}\\{f(x)>0}\end{array}\right.$或$\left\{\begin{array}{l}{x<0}\\{f(x)<0}\end{array}\right.$,
∴由图得,0<x<2或x<-2,
∴不等式的解集是(-∞,-2)∪(0,2),
故选:B.
点评 本题考查函数的奇偶性、单调性的综合应用,不等式的等价转化,考查数形结合思想.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
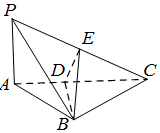 如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,DE垂直平分线段PC,且分别交AC、PC于D、E两点,PB=BC,PA=AB=1.
如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,DE垂直平分线段PC,且分别交AC、PC于D、E两点,PB=BC,PA=AB=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “m=-2”是“直线mx+(m-1)y-1=0与直线3x+my+2=0垂直”的充分不必要条件 | |
| B. | 已知a∈R,则“a<1”是“|x-2|+|x|>a”恒成立的必要不充分条件 | |
| C. | 设p,q是两个命题,若¬(p∧q)是假命题,则p,q均为真命题 | |
| D. | 命题p:“?x∈R,使得x2+x+1<0”,则¬p:“?x∈R,均有x2+x+1≥0” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com