
【题目】在四棱锥![]() 中,
中,![]() 为梯形,
为梯形,![]()
![]()
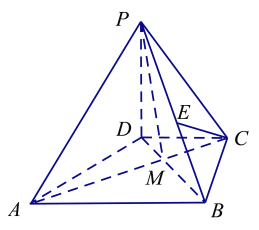
(1)点![]() 在线段
在线段![]() 上,满足
上,满足![]() 平面
平面![]() ,
,![]() ,求
,求![]() 的值
的值
(2)已知![]() 与
与![]() 的交点为
的交点为![]() ,若
,若![]() ,且平面
,且平面![]() 平面
平面![]() ,求二面角
,求二面角![]() 平面角的正切值
平面角的正切值
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图所示的几何体![]() 中,底面
中,底面![]() 为菱形,
为菱形, ![]() ,
, ![]() ,
, ![]() 与
与![]() 相交于
相交于![]() 点,四边形
点,四边形![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 底面
底面![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)若函数![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,求实数
上递增,求实数![]() 的值.
的值.
(2)若函数![]() 在定义域上不单调,求实数
在定义域上不单调,求实数![]() 的取值范围.
的取值范围.
(3)若方程![]() 有两个不等实数根
有两个不等实数根![]() ,求实数
,求实数![]() 的取值范围,并证明
的取值范围,并证明![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 为抛物线
为抛物线![]() 上一点.
上一点.
(1)若![]() ,求
,求![]()
(2)已知点![]() ,过点
,过点![]() 作直线
作直线![]() 分别交曲线
分别交曲线![]() 于
于![]() ,证明:在点
,证明:在点![]() 运动过程中,直线
运动过程中,直线![]() 始终过定点,并求出该定点.
始终过定点,并求出该定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】诚信是立身之本,道德之基,我校学生会创设了“诚信水站”,既便于学生用水,又推进诚信教育,并用“![]() ”表示每周“水站诚信度”,为了便于数据分析,以四周为一周期,如表为该水站连续十二周(共三个周期)的诚信数据统计:
”表示每周“水站诚信度”,为了便于数据分析,以四周为一周期,如表为该水站连续十二周(共三个周期)的诚信数据统计:
第一周 | 第二周 | 第三周 | 第四周 | |
第一周期 |
|
|
|
|
第二周期 |
|
|
|
|
第三周期 |
|
|
|
|
(Ⅰ)计算表中十二周“水站诚信度”的平均数![]() ;
;
(Ⅱ)若定义水站诚信度高于![]() 的为“高诚信度”,
的为“高诚信度”,![]() 以下为“一般信度”则从每个周期的前两周中随机抽取两周进行调研,计算恰有两周是“高诚信度”的概率;
以下为“一般信度”则从每个周期的前两周中随机抽取两周进行调研,计算恰有两周是“高诚信度”的概率;
(Ⅲ)已知学生会分别在第一个周期的第四周末和第二个周期的第四周末各举行了一次“以诚信为本”的主题教育活动,根据已有数据,说明两次主题教育活动的宣传效果,并根据已有数据陈述理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆:![]() 的离心率为
的离心率为![]() ,y轴于椭圆相交于A、B两点,
,y轴于椭圆相交于A、B两点,![]() ,C、D是椭圆上异于A、B的任意两点,且直线AC、BD相交于点M,直线AD、BC相交于点N.
,C、D是椭圆上异于A、B的任意两点,且直线AC、BD相交于点M,直线AD、BC相交于点N.
![]() 求椭圆的方程;
求椭圆的方程;
![]() 求直线MN的斜率.
求直线MN的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( ).
A. ![]() ,“
,“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
B. “![]() 且
且![]() 为真命题”是“
为真命题”是“![]() 或
或![]() 为真命题” 的必要不充分条件
为真命题” 的必要不充分条件
C. 命题“![]() ,使得
,使得![]() ”的否定是:“
”的否定是:“![]() ”
”
D. 命题![]() :“
:“![]() ”,则
”,则![]() 是真命题
是真命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com