
【题目】已知直线![]() 与圆
与圆![]() :
:![]() 交于
交于![]() 两点.
两点.
(1)求线段![]() 的垂直平分线的方程;
的垂直平分线的方程;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,求过点![]() 的圆
的圆![]() 的切线方程。
的切线方程。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
试题分析:(1)由题意,线段![]() 的垂直平分线经过圆的圆心
的垂直平分线经过圆的圆心![]() ,斜率为
,斜率为![]() ,可得线段
,可得线段![]() 的垂直平分线的方程;(2)利用
的垂直平分线的方程;(2)利用![]() ,求出圆心到直线的距离,利用点到直线的距离公式求出圆心到直线的距离,从而可求
,求出圆心到直线的距离,利用点到直线的距离公式求出圆心到直线的距离,从而可求![]() 的值;(3)用点斜式设出直线方程,相切可得
的值;(3)用点斜式设出直线方程,相切可得![]() ,注意讨论斜率不存在时,为本题易错点.
,注意讨论斜率不存在时,为本题易错点.
试题解析:(1)由题意,线段AB的垂直平分线经过圆的圆心![]() ,斜率为
,斜率为![]() ,
,
∴方程为![]() ,即
,即![]() ;
;
(2)圆![]() 可化为
可化为![]()
∵|AB|=2![]() ,∴圆心到直线的距离为
,∴圆心到直线的距离为![]() =
=![]() ,
,
∵圆心到直线的距离为![]()

![]()
![]() ,∴
,∴![]()
![]()
![]() ,∴
,∴![]()
(3)由题意,知点![]() 不在圆上.
不在圆上.
①当所求切线的斜率存在时,设切线方程为![]() ,即
,即![]()
由圆心到切线的距离等于半径,得![]()

![]() ,
,
解得![]() ,所以所求切线的方程为
,所以所求切线的方程为![]()
②当所求切线的斜率不存在时,切线方程为![]()
综上,所求切线的方程为![]() 或
或![]()


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,棱长为1的正方体![]() 中,点P是线段
中,点P是线段![]() 上的动点.当
上的动点.当![]() 在平面
在平面![]() ,平面
,平面![]() ,平面ABCD上的正投影都为三角形时,将它们的面积分别记为
,平面ABCD上的正投影都为三角形时,将它们的面积分别记为![]() ,
,![]() ,
,![]() .
.

(1)当![]() 时,
时,![]() ________
________![]() (用“>”或“=”或“<”填空);
(用“>”或“=”或“<”填空);
(2)![]() 的最大值为________.
的最大值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某网站的程序员中随机抽取![]() 名统计其年龄数据如下表:
名统计其年龄数据如下表:
年龄 | 23 | 26 | 27 | 30 | 32 | 34 | 38 |
人数 | 1 | 3 | 3 | 5 | 4 | 3 | 1 |
(1)求这![]() 名程序员的平均年龄及年龄的众数、中位数;
名程序员的平均年龄及年龄的众数、中位数;
(2)若这![]() 名程序员中年龄不超过
名程序员中年龄不超过![]() 岁,且学历是研究生及其以上有
岁,且学历是研究生及其以上有![]() 人,
人,![]() 岁以上且学历是本科及其以下有
岁以上且学历是本科及其以下有![]() 人,完成下面的列联表,并判断是否有
人,完成下面的列联表,并判断是否有![]() %的把握认为该网站程序员的学历与年龄有关.
%的把握认为该网站程序员的学历与年龄有关.
年龄≤30 | 年龄>30 | |
学历研究生及其以上 | ||
学历本科及其以下 |
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
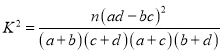 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
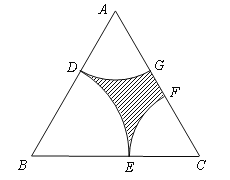
【题目】近年来,随着我市经济的快速发展,政府对民生越来越关注市区现有一块近似正三角形的土地![]() (如图所示),其边长为2百米,为了满足市民的休闲需求,市政府拟在三个顶点处分别修建扇形广场,即扇形
(如图所示),其边长为2百米,为了满足市民的休闲需求,市政府拟在三个顶点处分别修建扇形广场,即扇形![]() 和
和![]() ,其中
,其中![]() 与
与![]() 、
、![]() 分别相切于点
分别相切于点![]() ,且
,且![]() 与
与![]() 无重叠,剩余部分(阴影部分)种植草坪.设
无重叠,剩余部分(阴影部分)种植草坪.设![]() 长为
长为![]() (单位:百米),草坪面积为
(单位:百米),草坪面积为![]() (单位:万平方米).
(单位:万平方米).
(1)试用![]() 分别表示扇形
分别表示扇形![]() 和
和![]() 的面积,并写出
的面积,并写出![]() 的取值范围;
的取值范围;
(2)当![]() 为何值时,草坪面积最大?并求出最大面积.
为何值时,草坪面积最大?并求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P是抛物线C:![]() 上任意一点,过点P作直线PH⊥x轴,点H为垂足.点M是直线PH上一点,且在抛物线的内部,直线l过点M交抛物线C于A、B两点,且点M是线段AB的中点.
上任意一点,过点P作直线PH⊥x轴,点H为垂足.点M是直线PH上一点,且在抛物线的内部,直线l过点M交抛物线C于A、B两点,且点M是线段AB的中点.
(1)证明:直线l平行于抛物线C在点P处切线;
(2)若|PM|=![]() , 当点P在抛物线C上运动时,△PAB的面积如何变化?
, 当点P在抛物线C上运动时,△PAB的面积如何变化?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知M,N是焦点为F的抛物线y2=2px(p>0)上两个不同的点,线段MN的中点A的横坐标为![]() .
.
(1)求|MF|+|NF|的值;
(2)若p=2,直线MN与x轴交于点B,求点B的横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面ABCD,底部ABCD为菱形,E为CD的中点.
平面ABCD,底部ABCD为菱形,E为CD的中点.

(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)若∠ABC=60°,求证:平面PAB⊥平面PAE;
(Ⅲ)棱PB上是否存在点F,使得CF∥平面PAE?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高二年级组织外出参加学业水平考试,出行方式为:乘坐学校定制公交或自行打车前往,大数据分析显示,当![]() 的学生选择自行打车,自行打车的平均时间为
的学生选择自行打车,自行打车的平均时间为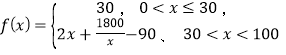 (单位:分钟) ,而乘坐定制公交的平均时间不受
(单位:分钟) ,而乘坐定制公交的平均时间不受![]() 影响,恒为40分钟,试根据上述分析结果回答下列问题:
影响,恒为40分钟,试根据上述分析结果回答下列问题:
(1)当![]() 在什么范围内时,乘坐定制公交的平均时间少于自行打车的平均时间?
在什么范围内时,乘坐定制公交的平均时间少于自行打车的平均时间?
(2)求该校学生参加考试平均时间![]() 的表达式:讨论
的表达式:讨论![]() 的单调性,并说明其实际意义.
的单调性,并说明其实际意义.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com