
����Ŀ�����������������о��õĿ��ٷ�չ������������Խ��Խ��ע��������һ������������ε�����![]() ����ͼ��ʾ������߳�Ϊ2���ף�Ϊ������������������������������������㴦�ֱ������ι㳡��������
����ͼ��ʾ������߳�Ϊ2���ף�Ϊ������������������������������������㴦�ֱ������ι㳡��������![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() �ֱ������ڵ�
�ֱ������ڵ�![]() ����
����![]() ��
��![]() ���ص���ʣ�ಿ�֣���Ӱ���֣���ֲ��ƺ.��
���ص���ʣ�ಿ�֣���Ӱ���֣���ֲ��ƺ.��![]() ��Ϊ
��Ϊ![]() ����λ�����ף�����ƺ���Ϊ
����λ�����ף�����ƺ���Ϊ![]() ����λ����ƽ���ף�.
����λ����ƽ���ף�.
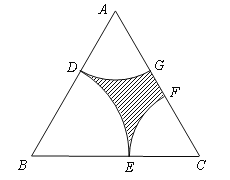
��1������![]() �ֱ��ʾ����
�ֱ��ʾ����![]() ��
��![]() ����������
���������д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����![]() Ϊ��ֵʱ����ƺ���������������.
Ϊ��ֵʱ����ƺ���������������.
���𰸡���1��![]() ��
��![]() ��
��![]() ����2��
����2��![]() ʱ����ƺ������������Ϊ
ʱ����ƺ������������Ϊ![]() ��ƽ����.
��ƽ����.
��������
��1����Ϊ![]() �����Կɵ��������εİ뾶��Բ�ĽǶ�Ϊ
�����Կɵ��������εİ뾶��Բ�ĽǶ�Ϊ![]() �������ε������ʽ�ɵô𰸣�
�������ε������ʽ�ɵô𰸣�
��2���������������ȥ������������ɵò�ƺ����������ö��κ����������ֵ.
��1��![]() ����
����![]() ��
��![]() ��
��
������![]() ��
�У�![]() �ij�Ϊ
�ij�Ϊ![]() ��
��
����![]() ��
��
ͬ����![]() .
.
��![]() ��
��![]() ���ص�����
���ص�����![]() ����
����![]() ����
����![]() .
.
���������ζ����������ڲ�����![]() ����
����![]() .
.
��2����![]() ��
��
��![]()
![]()
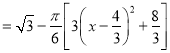 ��
��
�൱![]() ʱ��
ʱ��![]() ȡ�����ֵ��Ϊ
ȡ�����ֵ��Ϊ![]() .
.
�ʵ�![]() ��Ϊ
��Ϊ![]() ����ʱ����ƺ������������Ϊ
����ʱ����ƺ������������Ϊ![]() ��ƽ����.
��ƽ����.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Ա�ڶ�ij���ʵķ�ֳ������е���ʱ���֣�1�¡�2�¡�3�¸����ʵ������ֱ�Ϊ3��5��9����λ.Ϊ��Ԥ���Ժ���¸����ʵ���������ѡ����ģ��![]() ����ѡ����ģ��
����ѡ����ģ��![]() ������yΪ�����ʵ�������xΪ�·�����a��b��c��p��q��rΪ����.
������yΪ�����ʵ�������xΪ�·�����a��b��c��p��q��rΪ����.
��1����5�·ݼ���������32����λ������Ϊ�ĸ�ģ�ͽϺã���˵������.
��2��������ѡ���ģ�ͣ��Էֱ����4�¡�7�º�10�¸����ʵĵ������������Ӽ���������������ٶȵ������ʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() (
(![]() ������
Ϊ������![]() ����Ȼ�����ĵ���),������
����Ȼ�����ĵ���),������![]() �ڵ�
�ڵ�![]() �����ߵ�б��Ϊ
�����ߵ�б��Ϊ![]() .
.
������ʵ��![]() ��ֵ��
��ֵ��
������![]() �������ۺ���
�������ۺ���![]() �ĵ�����.
�ĵ�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2002�������ѧ�Ҵ���ڱ����ٿ�����������ҹ��Ŵ���ѧ����ˬ����ͼΪ�������.��ͼ�����ĸ�ȫ�ȵ�ֱ����������һ��С������ƴ�ɵ�һ����������(��ͼ)���С�����εı߳�Ϊ1���������εı߳�Ϊ5��ֱ���������н�С�����Ϊ![]() ����
����![]() ( )
( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ![]() �У�ֱ��
�У�ֱ��![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() Ϊ���������ڼ�����ϵ�У�ԲC�ļ����귽��Ϊ��
Ϊ���������ڼ�����ϵ�У�ԲC�ļ����귽��Ϊ��![]()
��1����ԲC��ֱ�����귽�̣�
��2����ԲC��ֱ��![]() ����
����![]() ���㣬���������Ϊ
���㣬���������Ϊ![]() ,��
,��![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��![]() ��Բ
��Բ![]() ��
��![]() ����
����![]() ������
������
��1��������![]() �Ĵ�ֱƽ���ߵķ�����
�Ĵ�ֱƽ���ߵķ�����
��2����![]() ����
����![]() ��ֵ��
��ֵ��
��3������2���������£������![]() ��Բ
��Բ![]() �����߷��̡�
�����߷��̡�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ϊ�˽�Ⱥ�����°������ʹ��������������䰴�ֲ�����ķ�ʽ�����˸õ���50��Ⱥ�ڣ����ǵ�����Ƶ����ʹ�ù������������ֲ����±���
����� | 20~29 | 30~39 | 40~49 | 50~60 |
Ƶ�� | 12 | 18 | 15 | 5 |
����ʹ�ù������� | 6 | 12 | 5 | 1 |
��1��������ͳ��������������![]() �����������ж��Ƿ���95%�İ�����Ϊ��40��Ϊ�ֽ����Ƿ�ʹ�ù��������в��죿
�����������ж��Ƿ���95%�İ�����Ϊ��40��Ϊ�ֽ����Ƿ�ʹ�ù��������в��죿
�������40�� | ���䲻����40�� | �ܼ� | |
����ʹ�ù������� | |||
������ʹ�ù������� | |||
�ܼ� |
����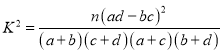 ��
��![]() .
.
| 0.25 | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
��2�������÷ֲ�����ķ�ʽ���������40���Ҿ���ʹ�ù���������Ⱥ����ѡ��6�ˣ��ٴ���6���������ȡ2�ˣ�����2����ǡ����1��������30~39��ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
��1�������x�IJ���ʽ![]() ��
��
��2���������![]() (��1��2)��
(��1��2)��![]() ���������ʵ��k��ȡֵ��Χ��
���������ʵ��k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ������
������![]() �϶����Լ�����
�϶����Լ�����![]() ��
��![]()
��1����![]() ʱ��������
ʱ��������![]() �ڵ�
�ڵ�![]() �������߷��̣�
�������߷��̣�
��2����![]() �������Сֵ���������Ӧ�ĵ�����꣮
�������Сֵ���������Ӧ�ĵ�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com