
 直线AB过抛物线x2=2py(p>0)的焦点F,并与其相交于A、B两点,Q是线段AB的中点,M是抛物线的准线与y轴的交点,O是坐标原点.
直线AB过抛物线x2=2py(p>0)的焦点F,并与其相交于A、B两点,Q是线段AB的中点,M是抛物线的准线与y轴的交点,O是坐标原点.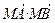 的取值范围;
的取值范围;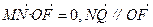 ;
;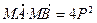 ,△ABN的面积的取值范围为[5
,△ABN的面积的取值范围为[5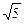 ,20
,20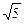 ]时,求该抛物线的方程.
]时,求该抛物线的方程.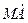 ·
·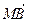 的取值范围是
的取值范围是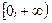 .
. 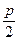 ),F(0,
),F(0,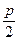 ).设直线AB的方程为
).设直线AB的方程为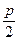 ,A(
,A( ,
,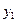 ),B(
),B(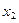 ,
,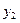 )
) ,
, ,Q(
,Q(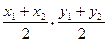 ). …………………………2分
). …………………………2分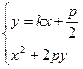 得
得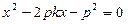 .
. +
+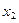 =2pk,
=2pk, ·
·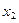 =-
=-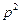 …………………………3分
…………………………3分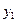
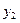 =
=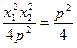
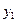 +
+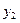 =k(
=k( +
+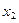 )+p=2pk
)+p=2pk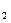 ÷p.
÷p.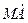 ·
·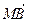 的取值范围是
的取值范围是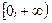 . …………………………4分
. …………………………4分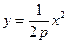 ,求导得
,求导得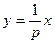 .
.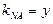
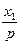
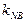 =y
=y 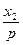 .
.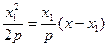 即
即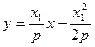 .
.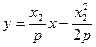 …………………………6分
…………………………6分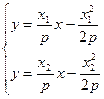 解得
解得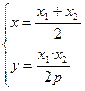 ∴N(
∴N( )
)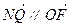 …………………………7分
…………………………7分 +
+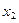 =2pk,
=2pk, ·
·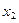 =-p
=-p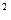
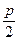 ). …………………………8分
). …………………………8分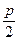 ) ∴
) ∴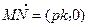
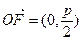 . ∴
. ∴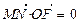 . …………………………9分
. …………………………9分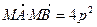 .又根据(Ⅰ)知
.又根据(Ⅰ)知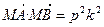
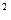 =p
=p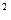 k
k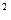 ,而p>0,∴k
,而p>0,∴k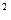 =4,k=±2. …………………………10分
=4,k=±2. …………………………10分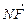 =(-pk,p),
=(-pk,p), 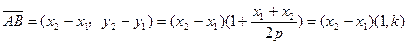
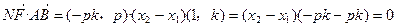
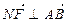 . …………………………11分
. …………………………11分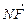 |=
|=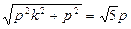 ,|
,|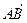 |=
|=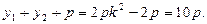
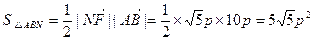 .
.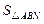 的取值范围是[5
的取值范围是[5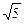 ,20
,20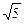 ].
].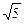 ≤5
≤5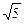 p2≤20
p2≤20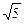 ,1≤p2≤4. …………………………13分
,1≤p2≤4. …………………………13分

科目:高中数学 来源:不详 题型:解答题
 应设计为多少?
应设计为多少?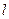 ,才能使建造这个隧道的土方工程量最小(半椭圆面积公式为
,才能使建造这个隧道的土方工程量最小(半椭圆面积公式为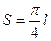 h)?
h)?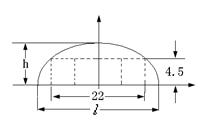
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
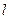 过抛物线的焦点F,交抛物线与A、B两点, 且
过抛物线的焦点F,交抛物线与A、B两点, 且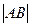 ="4p" ,求直线
="4p" ,求直线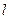 的方程.
的方程.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.(4,0) | B.(2,0) | C.(0,2) | D.(0,-2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com